Least Square & Normal Equation

본 포스팅의 모든 출처는 edwith의 고려대학교 주재걸 교수님의 "인공지능을 위한 선형대수" 강좌입니다

좋은 강의를 제공해주신 교수님께 감사드립니다 :)

[LECTURE] Least Squares Problem 소개 : edwith

앞서 작성한 포스트를 읽고 오시면 이해하는데 더 도움이 됩니다 :)

• 2022.02.18 - [통계] - 선형독립과 선형종속
• 2022.02.14 - [통계] - 회귀분석과 해의 존재성

앞선 포스팅에서 아래의 문제를 다뤘습니다.

$$ Ax = b $$

matrix $A$의 컬럼 벡터에 가중치($x$)로 선형 결합하여 만들 수 있는 공간을 Span 이라고 하며 이는 좌항에 해당하고, 우리가 만들고자 하는 벡터 $b$는 우항에 해당합니다.

그리고 $b$가 Span 안에 포함되는 경우 해 $x$가 존재한다고 하였습니다.

위의 예시 그림을 봅시다

matrix $A$에서 행의 수(샘플 수)가 m이고, feature의 수(컬럼 벡터 수)가 n입니다. 여기서 샘플 수인 m은 각 컬럼 벡터가 존재하는 공간의 차원 수입니다

그리고 우리가 일반적으로 다루는 선형 회귀 문제는 feature 수에 비해 샘플 수가 매우 많습니다(m >> n). 이런 경우 아래와 같은 이유로 해가 존재할 가능성이 매우 낮아집니다.

• matrix $A$의 각 컬럼 벡터는 m차원 공간 안에 있다
• matrix $A$의 컬럼 벡터 n개(위의 그림에서는 3)를 선형 결합하여 m차원에 존재하는 하나의 벡터인 $b$를 만들어야 한다

해당 문제는 m차원 공간을 다루고 있고, 컬럼 벡터 n개의 선형 결합으로 cover할 수 있는 공간(Span)은 매우 한정적일 것입니다. 그런데 벡터 $b$는 m차원 공간 상의 하나의 점이므로 위에서 언급한 공간(matrix $A$의 컬럼 벡터의 Span)에 포함될 가능성이 매우 낮을 것입니다.

즉, 위와 같은 상황에서 우리가 구하고자 하는 해인 $x$가 존재할 가능성이 매우 낮아집니다.

여기서 말하는 해는 $A$, $b$가 주어졌을 때 정확히 $b$를 맞출 수 있는 해 $x$를 의미합니다

그렇다면 해를 구할 수 없나요?

$Ax = b$를 정확히 일치시키는 해 $x$를 구할 수 없지만 최대한 근접하게 만드는 해는 구할 수 있을 것입니다. 여기서 "근접하다"를 측정할 때 사용되는 개념이 Least Square입니다.

그렇다면 구체적으로 "매우 근접한 해이다"의 기준은 무엇일까요?

바로 matrix $A$의 컬럼 벡터의 Span 안의 벡터 중 벡터 $b$와의 거리를 가장 짧게 만들 수 있는 $x$를 의미합니다.
거리는 직선 거리(euclidian distance)이며 이는 $Ax$와 $b$의 각 요소 간의 각 차이에 제곱을 취해 전체를 더한 다음 루트를 씌워 계산할 수 있습니다. (root of sum of square)

위의 예시에서 두 가지 해를 비교한다고 하였을 때 첫 번째 해가 직선 거리가 더 짧기 때문에 더 좋은 해라고 평가하는 것입니다

• 첫번째 해) $x = [-0.12, 16, -9.5]$ → $||Ax - b||$= 9.55
• 두번째 해) $x = [-0.4, 20, -20]$ → $||Ax - b||$= 12

즉, 무한히 많은 $x$ 중 우리가 찾고자 하는 최적해를 $\hat{x}$라고 표현한다면 아래의 문제를 푸는 것이 됩니다.

$$ \large \hat{x} = argmin_{x} ||b - Ax|| $$

Span 개념으로 최적해를 구해보자

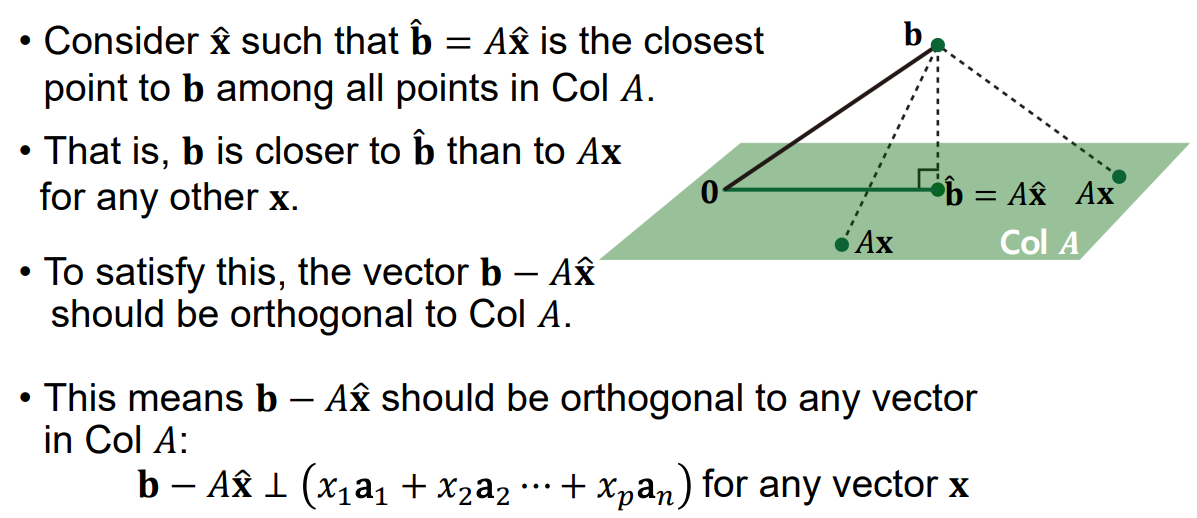
위의 그림을 통해서 기하학적으로 생각해보았을 때, 우리가 matrix $A$의 컬럼 벡터의 선형 결합으로 만들 수 있는 Span은 초록색 평면이라고 합시다. 우리는 matirx $A$의 컬럼 벡터에 적절한 가중치($x$)를 곱하여 벡터 $b$와 가장 가까운 $Ax$를 만들고 싶습니다. 

여기서 거리가 가장 짧다는 것은 $b$에서 Span에 수선의 발을 내린다는 의미가 됩니다. 그리고 이 수선의 발을 만들기 위해 matrix $A$의 컬럼 벡터에 취해야하는 가중치 $x$가 우리가 구하고자 하는 최적해  $\hat{x}$가 됩니다.

• $\hat{b}$ : 내린 수선의 발 (Span 안에 존재함)
• $\hat{x}$ : 수선의 발 $\hat{b}$를 만들기 위해 각 column 벡터에 취해야하는 weight, 즉 $A\hat{x} = \hat{b}$

여기서 한번 정리하면,

1. 우리는 $||b-Ax||$를 최소화하는 최적해인 $\hat{x}$를 구하려고합니다
2. 그리고 이를 기하학적으로 보았을 때 $Ax$가 존재하는 공간인 Span에 $b$가 내린 수선의 발 $\hat{b}$이 $A\hat{x}$됩니다 (→ $\hat{b} = A\hat{x}$ 문제가 됩니다)

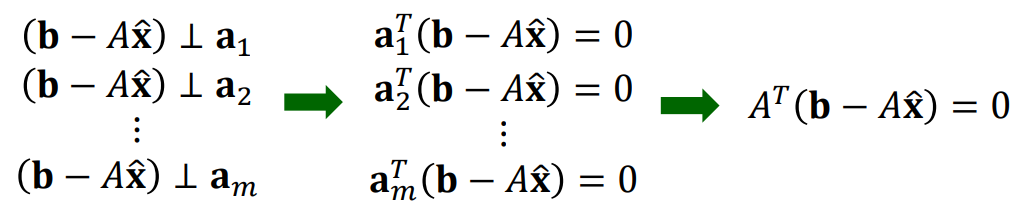
여기서 수선의 발이라는 특징에 주목할 필요가 있습니다

수선의 발 $\hat{b}$에서 벡터 $b$로 향하는 수선 벡터는 $b - \hat{b}$ ($A\hat{x}$)이고, 이는 Span과 수직이 됩니다. Span을 구성하는 모든 벡터들과 수선 벡터가 수직이라는 의미가 됩니다. 그리고 Span을 구성하는 벡터는 matrix $A$의 컬럼 벡터들이므로 위와 같이 문제가 바뀌게 됩니다.

$$ \large A^{T} (b - A\hat{x}) = 0 $$

 

정규방정식(Normal Equation)

이를 만족하는 최적 해 $\hat{x}$를 구하면 아래와 같습니다
이렇게 $A$와 $b$가 주어졌을 때, 오차인 $|| b - Ax ||$를 최소화하는 $x$를 구하는 방정식을 정규방정식이라고 합니다.

미분으로 최적해를 구해보자

위에서 우리가 구하고자 하는 최적해를 만족시키기 위한 식을 다시 한번 살펴봅시다. $||b - Ax||$를 최소화 하는 $x$가 우리가 구하고자 하는 최적해 $\hat{x}$였죠

$$ \large \hat{x} = argmin_{x} ||b - Ax|| $$ 
그런데 여기서 주목할 것은 $||b-Ax||$ 와 $||b-Ax||^2$는 비례 관계이므로 $||b-Ax||^2$를 최소화하는 문제로 바꿔도 된다는 것입니다. 

$$ \large \hat{x} = argmin_{x} ||b - Ax|| = argmin_{x} ||b - Ax||^2$$

 

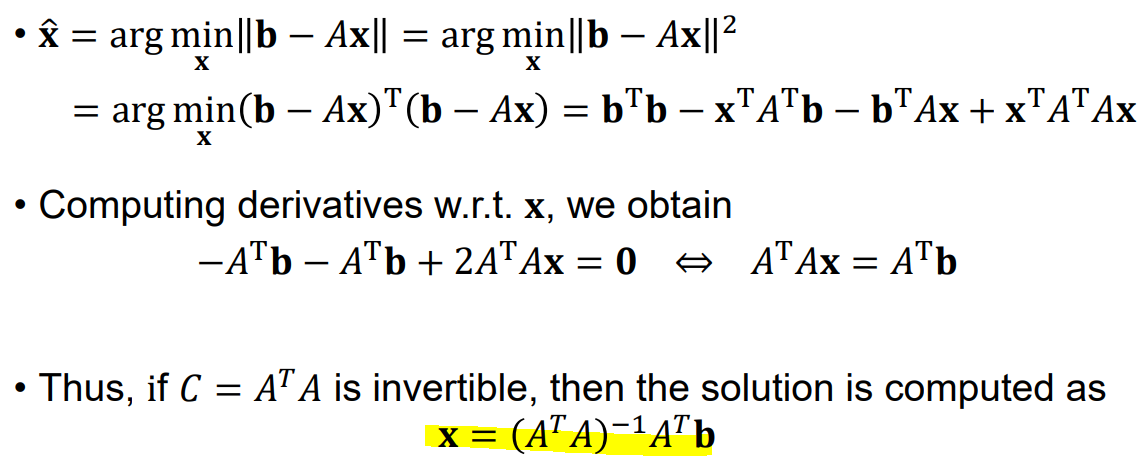
따라서, 해당 식을 $x$에 대해 미분하여 해당 값이 0이 되는 $x$값을 구하면 최적해 $\hat{x}$가 도출되고 이는 위의 정규방정식에서 도출한 최적해가 같습니다.

마치며

선형 회귀에서 최적해를 구하는 방법을 Span, Derivation 관점에서 살펴보았습니다.


▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼