MAB(Multi Armed Bandit)

인과추론(Causal Inference)

MAB(Multi Armed Bandit)

호재 P.B 2022. 3. 22. 00:58

개요

우리는 실험이 필요하다

Observational data에서는 실험군(좌), 대조군(우) 간 처치(원인)을 제외한 다른 특성이 다릅니다

이전 인과분석 방법론 포스트에서 우리는 교란 요인을 제거하고 원인 변수의 효과를 확인하기 위해서는 RCT(Radomized Control Trials)가 필요하다고 하였습니다. 관찰된 데이터(observational data)에서는 교란 요인의 영향이 존재할 가능성이 높고, 교란 요인에 의해 처치가 결정되는 자기 선택 편향(selection bias)이 발생합니다. 때문에 원인 변수(처치)를 기준으로 두 집단을 나누어도 처치 이외의 특성이 평균적으로 동일하지 않게 되고 결국 두 집단을 비교한 결과가 인과 효과가 아니라는 것입니다.(참고 : 교란 변수)

물론 교란 요인을 통제하여 인과 효과를 측정할 수 있습니다. 하지만, 교란 요인이 무엇인지 알기 힘들 뿐더러 모든 교란 요인을 통제한다는 것은 현실적으로 어렵기에 이렇게 통제를 통해 측정한 값도 편향이 발생할 가능성이 존재합니다.(참고 : 누락 편의(OVB))

Experimental data에서는 실험군(좌), 대조군(우) 간 처치(원인)을 제외한 다른 특성이 평균적으로 동일하게 됩니다

결국 명확한 인과 효과 측정을 위해서는 두 집단 간 원인 변수(처치)를 제외한 다른 특성은 평균적으로 동일하도록 데이터를 생성하고 두 집단을 비교하는 것이 가장 좋습니다. 여기서 데이터를 생성할 때 사용하는 개념이 RCT(Radomized Control Trials) 입니다. 집단을 랜덤하게 나누고 각각 처치를 다르게 할당하는 것이지요. 이렇게 하면 처치를 제외한 다른 조건은 평균적으로 동일하게 됩니다.

이 방법이 우리가 흔히 알고 있는 A/B test 입니다. 랜덤하게 두 집단을 나눈 후 한쪽은 처치를 가하고, 한쪽은 처치를 가하지 않은 상태에서 관측된 결과 변수를 비교하는 것이지요. 두 집단을 랜덤하게 나누고 처치를 할당하였기 때문에 처치에 영향을 미치는 교란 요인이 존재하지 않게 되며 결과적으로 자기 선택 편향이 발생하지 않아 명확한 인과 효과 추정이 가능합니다

A/B Test의 한계점

A/B Test를 활용하는 것은 좋지만 분명 단점이 존재한다는 사실도 알고 사용해야 합니다. 원점으로 돌아가서... 인과 효과를 측정하려는 이유는 뭘까요? 우리가 원하는 결과에 어떤 안(처치)이 더 좋은 효과를 갖는지 확인하고, 더 좋은 안을 채택하는 의사결정을 통해 비즈니스적으로 이득을 보기 위함입니다. 그런데 생각해보면 테스트 기간 동안 좋은 안을 적용 받은 집단과 좋지 않은 안을 적용 받은 집단이 필연적으로 존재하게 됩니다. 즉, 좋지 않은 안을 적용 받은 집단에게서는 테스트 기간 동안 비즈니스적으로 부정적인 효과가 나타날 것입니다.

여기서 A/B Test의 한계가 나타나게 됩니다. 애초에 어떤 안이 더 좋은지 모른 상태에서 A/B Test를 진행하기 때문입니다.

예를 들어 쇼핑몰 UI 설계를 위해 A/B Test를 진행한다고 합시다

유저에게 동일한 확률로 A안, B안 중 하나를 노출시킨다
각 안의 적용 받은 여부에 따라 유저들을 두 집단으로 나누고 30일 간 CTR, 구매 비율, 구매 금액의 평균을 비교하였다
A안이 (CTR이 20%높고, 구매 비율은 10%높고, 구매 금액도 평균적으로 5만원 높더라)라는 결과가 나왔다!!
A안이 더 좋으니 A안으로 UI를 설계하는 것이 좋겠다!

테스트를 한 결과 A안이 좋다는 인사이트를 얻을 수 있으나, B안을 적용받은 유저에게서는 테스트 기간(30일) 동안 유저 당 평균 5만원의 손실이 발생하게 됩니다. B안을 적용받은 유저들이 A안을 받았더라면 손실이 발생하지 않았을 것입니다. "탐색에 들어가는 비용", 즉 "기회 비용"이 존재할 수 밖에 없습니다. 이렇듯 A/B Test는 탐색하는 과정에서 발생하는 비용을 수반할 수 밖에 없는 한계점을 가지고 있습니다.

조금 더 똑똑하게 Test를 할 수 있는 방법이 없을까?

위에서 말한 것처럼 활용(A안 선택)을 위한 탐색 과정(A안, B안 중 어떤 것이 더 좋은가?)에는 비용(B안을 적용 받은 유저의 기회 비용)이 수반될 수 밖에 없습니다. "탐색"과 "활용"에는 trade-off 관계가 존재하는 것이죠.

탐색 : 어떤 안이 더 좋은가 실험하고 좋은 안을 찾아가는 과정
활용 : 좋은 안을 적용하여 이익을 꾀하는 것

우리는 조금 더 스마트하게 "탐색"에 들어가는 비용을 최소화 하고 좋은 안을 최대한 빠르게 선택하는 "활용"을 하고 싶습니다. 적절히 탐색하고 좋은 안을 빠르게 결정하려면 어떻게 하면 될까요?

MAB 개요

적절한 탐색(Exploration)과 활용(Exploitation)으로 최적의 수익을 내자!!

해당 문제를 풀어보고자 나타난 개념이 MAB(Multi Armed Bandit) 입니다. 최적의 수익을 위해서 여러 개의 선택지(Arm)중 어떤 것을 선택(Bandit)할까? 의 문제입니다

기원은 카지노에서 수익률이 다른 여러 슬롯머신 중 어떤 머신의 슬롯(Arm)을 당겨야(Bandit) 최대의 수익을 낼 수 있을까? 문제에서 비롯되었다고 합니다. 각 슬롯머신의 수익률을 모르는 상태에서 시작하기 때문에 여러 슬롯을 당겨보면서 "탐색"(Exploration)을 하고 가장 수익률이 좋다고 판단되는 슬롯을 찾아가서 "활용"(Exploitation)하는 과정입니다.

MAB 방법론

아래의 방법론을 설명하기에 앞서 간단히 notation을 정리하겠습니다

우리는 각 라운드($t$)마다 Arm 하나를 선택하여 실행하고, 얻은 보상($R$)을 기반으로 해당 Arm의 가치($Q$)를 계산할 것입니다. 그리고 계산된 각 "Arm의 가치"와 "어떤 rule(알고리즘)"을 기준으로 다음에 실행할 Arm을 선택합니다(이것이 아래에서 설명드릴 MAB 알고리즘의 종류들입니다). 그리고 다음 라운드로 넘어갑니다. 이를 매 라운드마다 반복합니다.

$t$ : 시도(라운드)
$R$ : 얻은 보상
$Q_t(a)$ : $t-1$ 라운드에 판단된 Arm $a$의 가치
$N_t(a)$ : $t-1$ 라운드 동안 Arm $a$가 선택된 횟수
$A_t$ : $t$ 라운드에 선택될 Arm

# greedy

"가장 간단한 방법은 존재하는 Arm을 모두 당겨보고, 그 중 기대 가치가 가장 높은 Arm을 선택하는 것입니다"

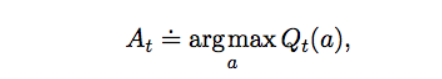
t-1라운드에서 측정된 Arm $a$의 기대 가치 $Q_t(a)$는 t-1 라운드 동안 Arm $a$로 얻은 보상의 평균을 의미합니다

$\sum_{i=1}^{t-1} {R_i \cdot 1_{A_i = a}}$ : t-1 라운드 동안 Arm $a$를 선택하여 얻은 보상의 합
$\sum_{i=1}^{t-1} {1_{A_i = a}}$ : t-1 라운드 동안 Arm $a$를 선택한 횟수

예를 들어 슬롯머신이 4개가 있습니다. 최초 탐색을 위해 슬롯머신의 수 만큼 총 4라운드 동안 한번씩 당겨, 다음과 같이 수익이 나왔다고 합시다. 이때 각 슬롯머신의 기대 가치($Q$)는 아래와 같습니다.

머신1 : 3000원
머신2 : 4000원
머신3 : 2000원
머신4 : 100원

그러면, 현재 머신2가 가장 기대 가치가 높기 때문에 다음 라운드인 5라운드에서는 머신2를 당기는 것입니다. 그래서 얻은 결과가 아래와 같은 경우 다음 6라운드에서는 어떤 머신을 선택할까요? 다시 가장 높은 기대 가치(평균)을 보이는 머신인 머신1을 선택합니다. 이를 모든 코인을 소진할 때까지 반복합니다.

머신1 : 3000원
머신2 : [4000원, 1000원] → 2500원
머신3 : 2000원
머신4 : 100원

매우 단순합니다. 하지만 이것이 최선의 방법일까요? 아닙니다. 처음에 가장 수익이 높게 나온 슬롯머신에 너무 많은 활용을 하게 되는 문제가 발생합니다. 다른 슬롯머신의 가치는 조금의 탐색만으로 결정해버리는 것입니다. "탐색"은 너무 적게, "활용"은 너무 많게 하는 전략입니다. 탐색을 거의 하지 못한 슬롯머신이 사실 숨겨진 보석일 수도 있습니다. 음.. 다른 슬롯머신들도 더 "탐색"을 할 필요성이 있어보입니다. 그러면 "탐색"을 할 때 어떤 기준으로 하는게 좋을까요?

# epsilon-greedy

탐색 기준을 epsilon($\epsilon; 0 < \epsilon < 1$)이라는 확률로 정하자!라는 것이 epsilon-greedy의 컨셉입니다.

다음 라운드에서 "탐색"을 할지, 아니면 현재 가장 좋아보이는 Arm을 당겨 "활용"을 할지 결정하는 파라미터입니다.

"각 라운드마다 탐색 할지 말지 $\epsilon$의 확률을 기준으로 정하고, 탐색 시에는 랜덤으로 슬롯머신을 정합니다"

$\epsilon$ 확률 만큼 "탐색" → 랜덤으로 Arm을 당겨 슬롯머신들의 가치를 탐색한다
$1-\epsilon$ 확률 만큼 "활용" → 현재 기준 가장 가치가 높은 Arm을 당긴다

# UCB(Upper Confidence Bound)

위의 epsilon-greedy 방법은 특정 확률 $\epsilon$에 따라 탐색을 할지 말지 정한 후, 탐색 시에는 랜덤하게 슬롯머신을 선택하였습니다. 탐색 시 모든 Arm을 선택할 기회가 동등하게 주어지는 것입니다.

탐색 시 조금 더 그럴듯하게 슬롯머신을 선택할 수 있는 방법은 없을까 고민이 됩니다. 탐색할 가치가 높은 슬롯머신을 골라서 선택하는 것이 좋을 것 같습니다. 그렇다면 탐색할 만한 가치는 어떻게 측정하는 것이 좋을까요?

"탐색된 정도가 적을수록, 기대 가치가 높을수록 탐색할 가치가 있지 않을까?"

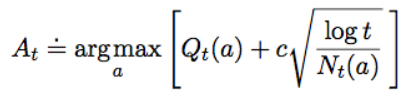
각 Arm들의 현재의 기대 가치와 탐색된 정도를 고려하여 탐색할 가치가 있는 Arm을 찾는 방법이 UCB 방법입니다. 수식을 보면 앞부분은 기대 이익을, 뒷 부분은 탐색된 정도를 역수(얼마나 덜 탐색되었는지)를 의미합니다.

$Q_t(a)$ : 현재 $t$라운드까지 Arm $a$의 기대 이익
$c \sqrt{\large\frac{log t}{N_t(a)}}$ : 이 항은 (현재 라운드 / Arm $a$가 선택된 횟수)와 비례한다
- Arm $a$가 적게 탐색되었을수록, 해당 값이 커지게 됩니다.
- 즉, 덜 탐색된 Arm은 값이 높아지며, 탐색될 가능성이 높도록 만들어주는 것입니다.
- 여기서 $c$는 해당 항에 얼마나 큰 가중치를 줄지 정하는 파라미터입니다

이해를 위해 아래의 예시를 보겠습니다. 2개의 슬롯머신이 있고 현재 총 8라운드를 거치며 다음과 같이 보상과 기대 가치가 계산되었다고 합시다. 그리고 다음 라운드에 탐색을 하게 되었다고 할 때, 어느 슬롯머신을 탐색하는 것이 좋을까요

머신1 : [2000원, 3000원, 2000원, 1000원, 500원, 3500원] → 기대 가치(평균) : 2000원
머신2 : [3000원, 1000원] → 기대 가치(평균) : 2000원

머신1은 머신2에 비해 여러 번 탐색되었기 때문에 현재 나온 기대 이익을 머신2에 비해 신뢰할 수 있을 것 같네요. 그런데 머신2는 머신1에 비해 아직 덜 탐색되었습니다. 그리고 기대 이익은 같은 상태입니다. 이런 상황에서 아직 덜 탐색된 머신2를 더 탐색하는 것이 좋겠지요.

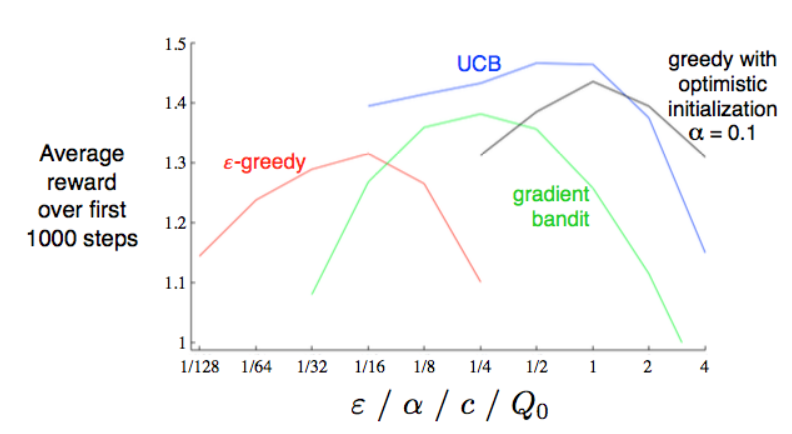
성능을 보았을 때도 UCB가 좋은 것을 알 수 있습니다

흐름을 정리해보자

탐색과 활용 측면에서 알고리즘의 한계점과 이를 보완하기 위한 방법 중심으로 정리해보면 아래와 같습니다.

MAB 알고리즘	요약	한계점
greedy	기대 이익이 높은 것에 몰빵하자!	탐색이 충분하지 않다
epsilon-greedy	특정 확률로 탐색을 하자	탐색할 Arm 선정 시 동일한 확률로 선정(랜덤)
UCB	탐색을 할 때, 가치가 높은 Arm을 선택하자 → 기대 가치와 탐색된 정도를 같이 고려하자

마치며

MAB의 개념을 공부하고 정리하면서 좋은 자료(아래의 링크)를 많이 접할 수 있었습니다.

좋은 자료를 작성해주신 제작자분들께 감사를 표합니다!

Reference

▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼