| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Python
- OVB
- simple linear regression
- 크롤링
- LU분해
- rct
- 사영
- least square estimation
- 잔차의 성질
- confounder
- backdoor adjustment
- Omitted Variable Bias
- 네이버 뉴스
- HTML
- residuals
- 머신러닝
- 인과 추론
- 예제
- 교란변수
- Instrumental Variable
- Sharp RD
- 회귀불연속설계
- 선형대수
- 단순선형회귀
- 인과추론
- causal inference
- 최소제곱법
- 교란 변수
- 통계
- 누락편의
- Today
- Total
Always awake,
인과 추론을 어렵게 하는 요소(교란 변수) 본문
앞의 포스팅을 읽고 오시는 것이 좋습니다 :)
인과 추론이 어려운 이유
동일 조건 맞추기? 자 어떤 상황을 생각해봅시다. 회사에서 매출 증대를 위해 프로모션 상품을 개시했다고 합시다. 여기서 우리가 확인할 것은 원인(프로모션 상품)과 결과(매출)의 관계입니다.
everyday-tech.tistory.com
앞선 포스팅에서 인과 관계를 확인하기 위해서는 비교하는 두 집단의 성질이 동일해야 하며, 현실 세계에서 이것이 만족되지 않는 경우가 대부분이라고 말씀드렸습니다. 외부 영향을 효과적으로 제거해야 두 사건의 인과 관계를 확인할 수 있습니다. 그렇다면 어떠한 경우 인과 관계가 아닌 외부 영향이 발생할까요?
상관 관계는 인과 관계가 아니다(Correlation is Not Causation). 두 사건이 상관성이 매우 높아도 이는 두 사건 간 인과 관계가 아니라 외부 영향에 의한 상관 관계일 가능성이 높습니다. 이렇게 사건 간의 연관성을 Association이라고 하는데 우리의 관심사에 따라 두 가지로 나누어 볼 수 있습니다.
- Causal Association : 실험자(분석가)가 측정하고자 하는 두 사건 간의 인과 관계
- Non-Causal Association : Causal Association 이외의 두 사건 간 상관성(제거 해야하는 외부 영향)
우리가 알고자 하는 인과 관계는 Causal Association이고, 그 이외에 Causal Association으로 착각하게 만드는 두 사건 간 상관 관계는 Non-Causal Association입니다. 단순히 두 사건을 비교하여 나오는 상관 관계는 Causal Association과 Non-Causal Association 이 합쳐진 것입니다. 그렇기에 두 사건을 단순 비교해서 나온 결과를 인과 관계로 착각하면 안됩니다.
두 사건 간에 인과 관계를 확인하기 위해서는 Non-Causal Association을 제거한 Causal-Association을 확인해야합니다..
Non-Causal Association이 발생하는 경우는 여러 가지가 있는데 본 포스팅에서는 교란 변수(Confounder)라는 것에 의해 생긴 Non-Causal Association에 대해 설명하고 어떻게 제거할 수 있는지 확인해보겠습니다.
교란 변수(Confounder)

가장 대표적인 경우가 교란 변수입니다.(앞의 포스팅에서 예시로 든 "프로모션 구매 여부가 매출 증가에 원인이 될까?"라는 주제에서 "충성도"가 교란 변수에 해당합니다)
교란 변수는 우리가 원인이라고 생각하는 것과 결과라고 생각하는 것에 동시에 영향을 주는 변수입니다. 두 변수에 동시에 영향을 주기 때문에 두 변수 간에 상관 관계가 생기게 됩니다. 이러한 교란 변수는 원인, 결과 간에 Non-Causal Association을 만들기 때문에 원인, 결과에 해당하는 두 변수를 단순 비교하는 경우 상관성이 나타납니다.
프로모션 구매 여부(원인)가 매출 증가(결과)에 미치는 인과 관계를 확인하기 위해 프로모션을 구매한 집단, 구매하지 않은 집단 간의 매출을 비교한다고 합시다.
여기서 교란 변수로 인해 애초에 공정한 비교가 불가능해집니다. 프로모션 구매 자체가 충성도라는 변수에 의해 영향을 받으므로, 프로모션을 구매한 집단에 충성도가 높은 고객이 많을 것이고 프로모션을 구매하지 않은 집단에 충성도가 낮은 고객이 많을 것입니다. 고객이 지닌 특성인 충성도에 따라 프로모션 구매가 정해지는 "자기 선택"이 존재하는 것이죠.
그리고 충성도는 매출에 영향을 미치므로 두 집단 간에 당연히 매출 차이가 존재합니다. 이 매출 차이는 프로모션 구매 여부(원인)에 의한 차이가 아닌 충성도(교란 변수)에 의한 차이입니다. 극단적으로 고객의 충성도(교란 변수)에 의한 Non-Causal Association을 고려하지 않은 채 단순히 비교를 한다면 프로모션 구매가 매출에 아무런 영향을 미치지 않거나 영향이 적음에도 영향을 미친다! 라고 판단할 수 있습니다.
이렇듯 실험자는 인과 효과 측정을 위해 원인(프로모션 구매 여부)을 기준으로 두 집단으로 나누고 그 이외 성질은 동일하기를 기대하지만, 현실에서는 교란 변수가 많기 때문에 두 집단의 특성이 동일하지 않은 경우가 많습니다.
교란 변수의 영향을 제거하려면
그렇다면 교란 변수가 존재하는 경우 원인과 결과의 인과 관계를 확인할 수 없는걸까요? 방법이 있습니다. 특성이 유사한 객체끼리 비교하는 방법입니다.(여기서는 충성도가 비슷한 고객끼리 비교하는 것이죠) 프로모션을 구매한 집단과 구매하지 않은 집단에서 충성도가 비슷한 고객끼리 매칭해서 매출을 비교하면 됩니다. 그러면 충성도가 프로모션 구매 여부(원인)와 매출(결과) 사이에서 만드는 Non-Causal Association을 제거할 수 있습니다. 즉, 교란 요인에 해당하는 조건을 동일하게 맞추고 프로모션 구매 여부(원인)에 따른 매출(결과)만을 비교하는 것이기에 인과 관계를 측정하는 것이라고 할 수 있습니다.
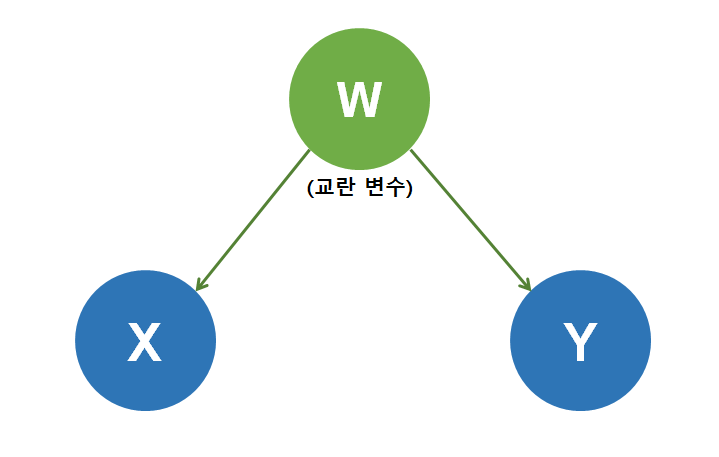
이를 확률로 표현하면 다음과 같습니다. 여기 $X$,$Y$,$W$ 변수가 있습니다. 그리고 $X$, $Y$에 $W$는 동시에 영향을 주는 교란 변수입니다. 교란 변수가 만드는 Non-Causal Association을 제거하기 위해서는 $W$를 통제해야하는데 이것은 확률적으로 조건부 확률을 만드는 것과 같습니다. 즉, $W$를 통제하였을 때, $X$와 $Y$가 독립이 된다면 $W$에 의한 Non-Causal Association을 제거하였다는 의미입니다. 한번 확인해보겠습니다.
1. bayesian network factorization
- $p(X,Y,W) = p(Y|W,X)p(X|W)p(W)$
- 여기서 $X$는 $Y$에 직접적인 영향을 미치지 않으므로 $p(Y|W,X)$가 $p(Y|W)$가 됩니다.
- $p(X,Y,W) = p(Y|W)p(X|W)p(W)$
2. 교란 변수 W에 대한 조건부 확률
- $p(X,Y|W) = \large{p(X,Y,W) \over p(W)}$
- 분자에 1번에 의해 도출된 식을 대입
- $\large{p(X,Y,W) \over p(W)} = \frac{p(Y|W)p(X|W)p(W)}{p(W)}=$ $p(Y|W)p(X|W)$
- 즉, $p(X,Y|W)=p(Y|W)p(X|W)$
위와 같이 $W$가 교란 변수인 경우 $W$를 통제하면 그 영향을 받은 두 변수는 독립이 됩니다.
즉, 교란 변수를 통제하면 교란 변수가 만드는 상관 관계(Non-Causal Association)을 제거할 수 있습니다.
교란 변수 영향 제거 예제
감이 안 온다면 예제를 통해 확인해봅시다. 아래와 같은 관계에서 교란 변수를 통제하였을 때 우리가 원하는 인과 관계인 $X$ → $Y$ (-2) 를 측정할 수 있는지 확인해보겠습니다(교란 변수 $W$가 $X$와 $Y$에 각각 미치는 3과 9의 영향을 제거해야 합니다) 변수 간 영향을 측정하기 위해 python3의 statsmodel의 회귀 모델을 사용하겠습니다.

데이터 생성
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as sm
np.random.seed(777) # 동일한 결과를 위해 시드 설정
num = 500 # 데이터 수
W = np.random.normal(size = num)
# X는 W의 영향을 받습니다.
X = 3.0 * W + np.random.normal(size = num)
# Y는 X와 W의 영향을 받습니다.
Y = 9.0 * W + -2.0 * X + np.random.normal(size = num)
data = pd.DataFrame({'X' : X, 'W' : W, 'Y' : Y})
단순히 $X$와 $Y$의 상관 관계 측정

단순히 scatter plot으로 $X$와 $Y$의 관계를 보았을 때 $X$가 증가함에 따라 $Y$가 증가하는 경향이 있습니다. 실제로 인과 관계로는 $X$가 $Y$에 -2 만큼의 영향을 미치기 때문에 $X$가 증가함에 따라 $Y$가 감소해야하는데 말이죠.
$X$와 $Y$를 적절한 통제 없이 단순 비교하는 경우 교란 변수 $W$의 영향도 포함되었기 때문에 실제 인과 관계와 완전히 다른 결과가 나올 수 있습니다. (이 scatter plot은 Causal Association과 Non-Causal Association이 합쳐진 상관 관계를 의미하는 것입니다)
# X와 Y를 단순 비교
sm.ols('Y ~ X', data).fit().summary()
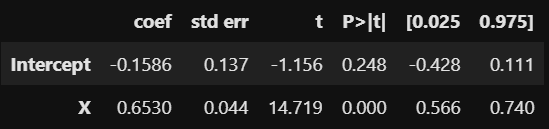
그러면 이제 회귀 모델로 $X$가 $Y$에 미치는 영향을 측정해보겠습니다.
$X$의 회귀 계수를 살펴보면 0.65이고 p-value가 0.000으로 유의한 영향을 미치는 것을 알 수 있습니다. 하지만 이 값은 우리가 측정하고자 하는 실제 인과 관계인 -2와 매우 다른 값입니다. $X$ 가 $Y$에 미치는 인과 관계(Causal Association)와 교란 변수$W$가 $X$와 $Y$ 사이에 만든 상관 관계(Non-Causal Association)이 합쳐진 영향이기 때문입니다.
교란 변수 $W$를 통제하여 $X$와 $Y$의 인과 관계 측정
이번에는 위에서 설명드린 교란 변수에 의한 Non-Causal Association을 제거하는 방법으로 교란 변수를 통제하여 $X$와 $Y$ 간의 인과 관계를 측정해보겠습니다. 회귀 분석에서 교란 변수를 통제하기 위해서는 독립 변수 항에 교란 변수를 추가하면 됩니다.
# 교란 변수(W)를 독립 변수에 추가하여 통제
sm.ols('Y ~ X + W', data).fit().summary()

교란 변수를 통제하자 각 변수가 Y에 미치는 영향이 어느 정도 실제 관계와 유사하게 나왔습니다.
- $X$ → $Y$ (측정하고자 하는 인과 관계) : 실제로는 -2만큼 영향을 미침. 회귀 계수가 -1.97로 유사하며 통계적으로도 유의함; 잘 추정됨
- $W$ → $Y$ (교란 변수가 결과 변수에 미치는 영향, 현재 분석의 관심사는 아님) : 실제로는 9만큼 영향을 미침. 회귀 계수가 -8.89로 유사하며 통계적으로도 유의함; 잘 추정됨
위의 예시에서 보았듯 회귀 모델이 추정하는 것은 상관 관계(Association)입니다. 실제로 인과 관계를 측정하기 위해서는 상관 관계 중 Non-Causal Association이 무엇인지 파악하고 이를 제거한 Causal Association을 측정하기 위한 고민이 필요합니다.
이처럼 단순히 두 변수로 회귀식을 구성하고 회귀 모델로 추정한 결과를 인과 관계라고 판단하는 것은 오류를 범할 가능성이 높습니다. 회귀 모델은 두 변수의 상관 관계(Association)을 추정해주는 "통계적 도구"이기 때문이죠. 두 변수의 인과 관계를 추정하기 위해서는 외부 영향이 어떤 것이 있는지, 어떻게 통제해야하는지 고민하는 작업이 반드시 필요합니다. 이를 회귀식에 반영하는 것은 분석가의 역량이며 여러 상황에 대한 이해(도메인 지식)가 밑받침되어야 합니다.
마치며
인과 관계 추정을 어렵게 하는 가장 흔한 요소인 교란 변수에 대해 설명을 드렸습니다.
교란 변수 말고도 인과 관계 추정 시 고려할 사항이 많은데요
collider라는 것에 대해서도 곧 포스팅을 진행하려 합니다.
긴 글 읽어주셔서 감사합니다 :D
▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼
'인과추론(Causal Inference)' 카테고리의 다른 글
| [인과 추론 발표] 2021 Summer Session On Causal Inference (0) | 2021.07.16 |
|---|---|
| backdoor adjustment (0) | 2021.07.12 |
| 인과 추론을 어렵게 하는 요소(Collider) (0) | 2021.06.05 |
| 인과 추론이 어려운 이유 (0) | 2021.05.18 |
| 인과 관계를 잘 알아야 하는 이유 (2) | 2021.05.11 |




