Orthogonal 벡터 만들기

orthogonal 개념

두 벡터가 "orthogonal하다"라는 것은 수직이라는 의미입니다.

두 벡터의 내적은 아래와 같으므로, orthogonal 한 두 벡터의 내적 값은 0 ($cos(\theta) = 0$)이 됩니다.

$$u \cdot v = |u| |v| cos(\theta)$$

 

orthogonal한 벡터 만들기

하나의 벡터 $u$가 주어져 있고, 여기에 orthogonal하지 않은 벡터 $v$를 추가한다고 합시다

그리고 추가한 벡터 $v$로 기존에 있던 $u$와 orthogonal한 벡터를 만들고 싶다면 어떻게 하면 좋을까요?

이 두 개의 벡터 $u$, $v$를 이용하여 $u$에 orthogonal한 새로운 벡터를 만들 수 있습니다!

 

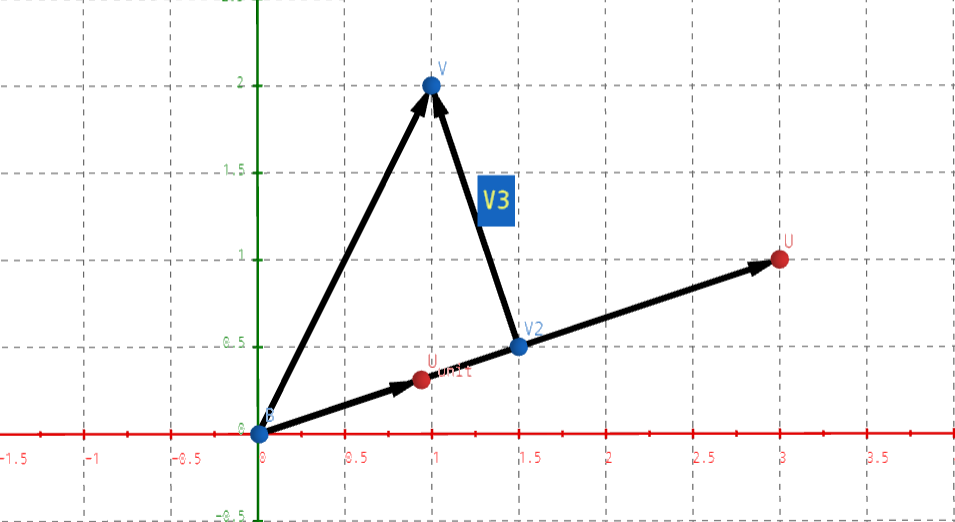
아래와 같이 2차원 평면에 $u = [3,1]$가 있고, 벡터 $v = [1,2]$를 추가하였습니다.

보이는 것처럼 두 벡터는 수직이 아니므로 orthogonal하지 않습니다

여기서 우리는 벡터 $v$에서 벡터 $u$로 수선의 발 $v_2$을 내릴 것입니다. 아래와 같이 말이죠

그렇게 되면, 우리는 $v_2$에서 $v$로 향하는 벡터를 구할 수 있게 되고 이는 기존에 존재한 벡터 $u$와 수직(orthogonal)이 됩니다. 해당 벡터를 $v_3$라고 한다면, $v_3 = (v - v_2)$와 같이 구할 수 있습니다.

 

그런데 여기서 $u$에 orthogonal한 벡터인 $v_3$를 구하기 위해서는 $v_2$가 필요합니다. 어떻게 구할 수 있을까요?

 

그림에서 보이는 것처럼 $v_2$는 $u$와 방향이 같은 벡터이기 때문에 $u$의 길이를 늘리거나 줄인다면 $v_2$를 만들 수 있습니다. 즉, 어떤 상수항 c를 $u$에 곱해주면 $v_2$를 만들 수 있습니다 (c는 상수)

$$v_2 = c u$$  

 

그렇다면 상수 c는 어떻게 구할 수 있을까요?

$u$와 방향이 같은 길이가 1인 unit 벡터 $u_{unit}$을 구하고 그 벡터에 $v_2$의 길이인 $|v_2|$를 곱해주면 됩니다.

아래의 식을 보면 위에서 말씀드린 상수항 c는 $\large\frac{|v_2|}{|u|}$가 되는 것이죠.

$$v_2 = |v_2| u_{unit} = |v_2| \frac{u}{|u|} = \frac{|v_2|}{|u|} u$$

이제 마지막으로 $|v_2|$ 만 구하면 $v_2$를 구할 수 있겠네요

답은 바로 위에서 보이는 직각 삼각형에 있습니다. 벡터 $u$와 $v$ 사이의 각도를 $\theta$라고 한다면, 삼각 함수 공식을 이용하여 $|v_2|$를 구할 수 있습니다.

$$|v_2| = |v| cos(\theta)$$

자, 최종적으로 식을 대입해보면 아래와 같습니다

$$v_2 = \frac{|v_2|}{|u|} u = \frac{|v| cos(\theta)}{|u|} u = cos(\theta) \frac{|v|}{|u|}  u$$

 

여기서 $cos(\theta) = \large\frac{u \cdot v}{|u||v|}$ 이고, $|u|^2 = u \cdot u$ 이므로, 아래와 같이 식이 변형됩니다.

$$v_2 = cos(\theta) \frac{|v|}{|u|} u = \frac{u \cdot v}{|u||v|}\frac{|v|}{|u|} u = \frac{u \cdot v}{|u|^2}u = \frac{u \cdot v}{u \cdot u} u$$

이제 진짜 진짜 마지막으로! 처음에 말씀 드린 $v_3 = (v - v_2)$를 이용하여 $u$와 orthogonal한 벡터를 만들 수 있게 됩니다

$$v_3 = v - \frac{u \cdot v}{u \cdot u} u$$

 

코드를 통한 예제

위의 두 벡터를 코드를 통해서 계산해보겠습니다

우선 numpy를 이용하여 위의 두 벡터 $u$, $v$를 만들어 줍니다.

import numpy as np

u = np.array([3,1])
v = np.array([1,2])

$v$에서 $u$에 수선의 발을 내린 $v_2$를 만들어 줍니다. 위의 수식을 참고하세요 :) 

# 새로 추가된 v를 u에 사영(수선의 발) 시키자
v2 =  (u.dot(v) / u.dot(u)) * u
print('vector v2 :', v2)

 

그리고, $v_2$와 $v$를 이용하여, $u$와 orthogonal한 벡터 $v_3$를 만들어 줍시다

# u와 orthogonal한 벡터를 만들자 
v3 = v - v2
print('vector v3 :', v3)

최종적으로 내적을 이용하여 $v_3$와 $u$가 orthogonal한지 확인합니다. 

내적 값이 0인 것으로 보아 orthogonal한 것을 알 수 있습니다 :)

# orthogonal한지 확인
print(u.dot(v3))

마치며

기존 벡터에 새로운 벡터를 추가할 때, orthogonal한 벡터를 만드는 방법에 대해 알아보았습니다

감사합니다.

 

 

▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼