| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 인과 추론
- 회귀불연속설계
- 인과추론
- 잔차의 성질
- 머신러닝
- simple linear regression
- Instrumental Variable
- rct
- 네이버 뉴스
- 선형대수
- 크롤링
- residuals
- LU분해
- OVB
- 단순선형회귀
- confounder
- 교란 변수
- 사영
- 통계
- least square estimation
- Omitted Variable Bias
- causal inference
- HTML
- backdoor adjustment
- Python
- 최소제곱법
- 교란변수
- 예제
- 누락편의
- Sharp RD
- Today
- Total
Always awake,
Transformer 행렬 연산 #1 Encoder 본문
"개인적으로 트랜스포머를 행렬 연산으로 이해하기 위해 작성한 포스트입니다"
트랜스포머를 공부하다 보면 개념적으로는 이해가 되는데, 아래 내용들이 머릿 속에서 잘 그려지지 않아 이해해보려 합니다!
- 전체 흐름이 어떻게 되는지
- 각 연산(Layer)마다 Tensor 형태가 어떻게 변하는지 (Input, Output)
- 행렬 연산으로는 어떻게 처리되는지
본 글에서는 Transformer 의 구조, 개념, 각 층의 상세한 수식 및 의미는 아래 첨부한 글에 나와 있어 생략하고,
행렬 연산을 통해 Tensor 의 형태가 어떻게 변해가는지 위주로 작성하였습니다!
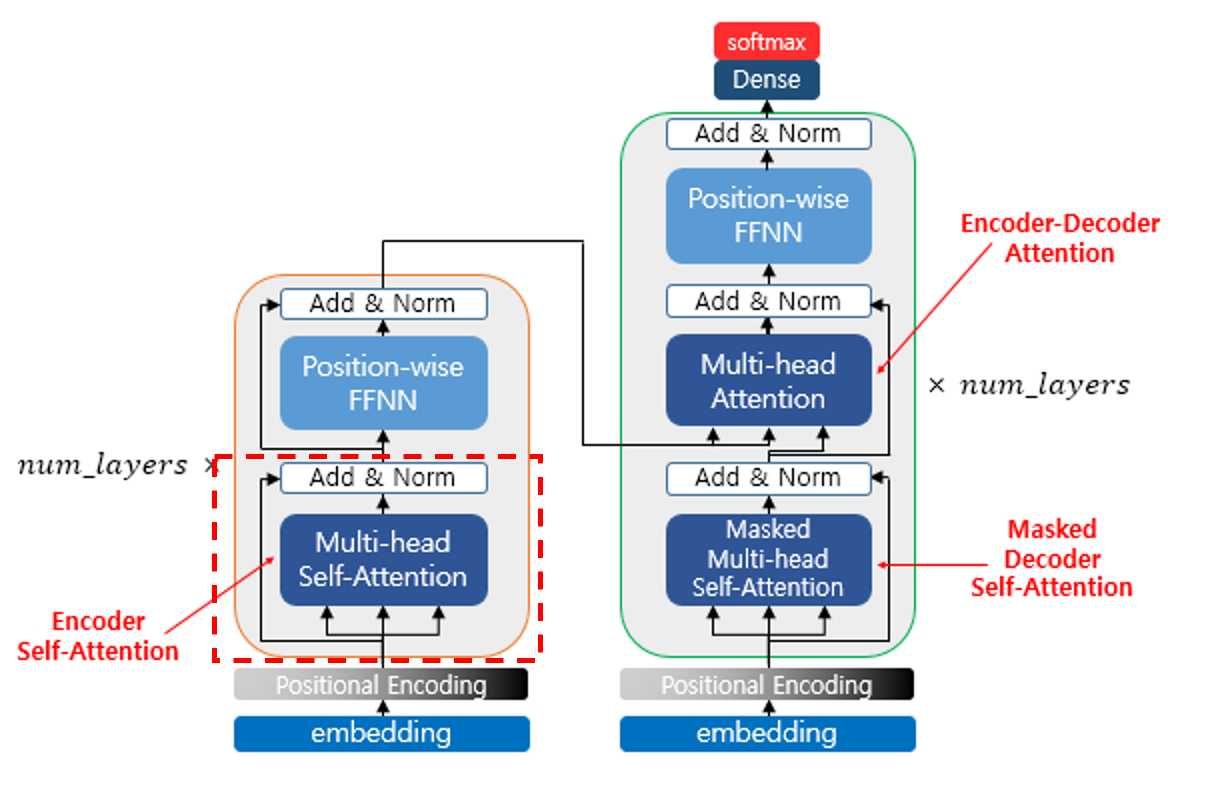
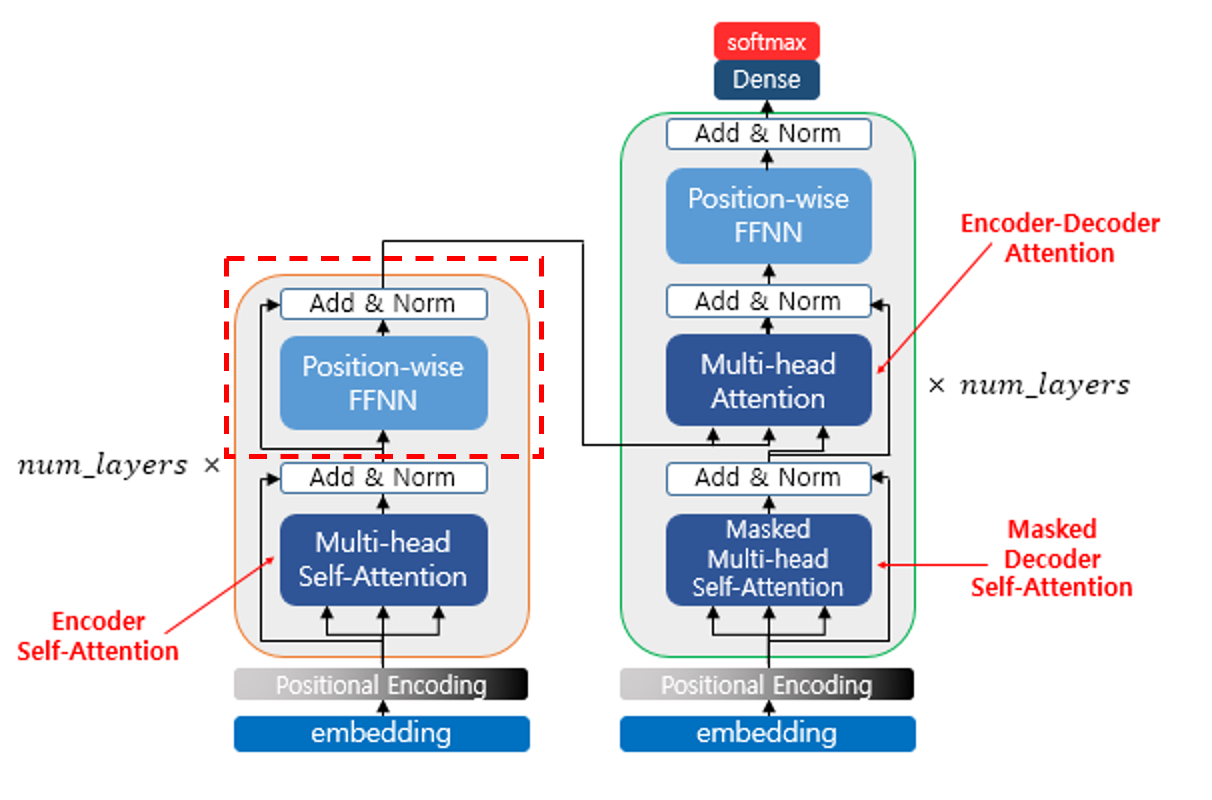
Transformer 구조

출처: https://wikidocs.net/217018
그래도 Transformer 구조는 간단하게나마 알아야 하기에 잠깐 설명하겠습니다!
Transformer 는 Encoder - Decoder 구조로 되어 있습니다.
Encoder, Decoder 에 들어가는 Input 공통적으로 1) Embedding, 2) Positional-Encoding 과정을 거칩니다
그리고 Encoder, Decoder 는 각각 크게 보면,
Encoder 는 1) Multi-Head Self-Attention 층, 2) Position-Wise FFNN 층 이 있습니다.
Decoder 는 1) Masked Multi-Head Self-Attention 층, 2) Cross Multi-Head Attention 층, 3) Position-Wise FFNN 층 이 있습니다.
그리고 각 층의 출력 후에는 Add & Norm 층이 있는데 Residual Connection 과 Layer Normalization 입니다.
Residual Connection 은 Input 과 Output 을 더하는 연산을 의미합니다.
예를 들어, Multi-Head Self-Attention 의 출력 후에 있는 Residual Connection 은 아래와 같습니다.
$$ResidualConnection(x) = x + MultiHeadSelfAttention(x)$$
Layer Normalization 은 Standard-Scaling 한 값과 $\gamma$, $\beta$ (학습 가능한 파라미터) 로 정의됩니다.
$$LayerNormalization(x) = \gamma \ StandardScaling(x) + \beta$$
행렬 연산으로 보기
이제 본 글의 목적인 행렬 연산으로 위의 과정이 어떻게 처리되는지 살펴보겠습니다.
아래의 그림에서 학습해야 하는 행렬(가중치) 는 점선 테두리로 표시하였습니다.
그리고 여러 파라미터가 나오는데, 각각의 의미와 그림에 사용한 값을 설명드리겠습니다.
(쉽게 이해하기 위해 그림에 나오는 차원 수는 다소 작게 설정하였습니다)
| Notation | 설명 | 그림에서 표현한 값 | Transfomer 기본 모델 값 |
| $seq\_len$ | 문장의 길이 (문장에서 토큰 수) | 3 | - |
| $d_{model}$ | Multi-Head Self Attention 층에서 토큰 벡터 차원수 | 8 | 512 |
| $n_{head}$ | Multi-Head Self Attention 층에서 Head 갯수 | 4 | 8 |
| $d_v$ | Multi-Head Attention 층 하나의 Head 에서 토큰 벡터 차원 수 (Value 에 해당) | 2 | 64 |
| $d_k$ | Multi-Head Attention 층 하나의 Head 에서 토큰 벡터 차원 수 (Key, Query 에 해당) | 2 | 64 |
| $d_{ff}$ | FFNN 층에서 토큰을 표현하는 벡터 차원 수 | 12 | 2048 |
Transformer Encoder
Encoder 부분부터 봅시다!
Embedding & Positional Encoding

빨간색 박스가 쳐져 있는 부분에 대한 설명입니다
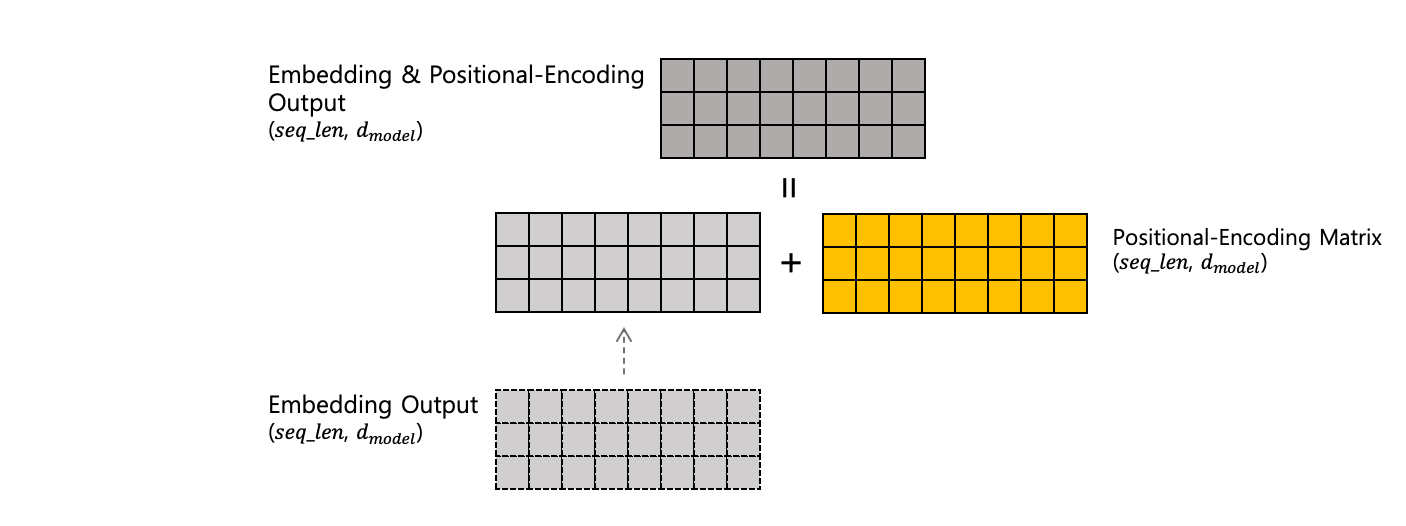
Embedding Output: $(seq\_len, d_{model})$ 형태의 행렬입니다. 각 $seq\_len$ 개의 토큰이 $d_{model}$ 의 차원으로 표현되어 있습니다. Embedding Output 의 각 element 는 랜덤으로 초기화 되고, 학습을 진행하며 값이 변경된다고 합니다 (Learnable Parameter). 자세한 내용은 조금 더 찾아봐야겠습니다!
Positional Encoding: Embedding Output $(seq\_len, d_{model})$ 에 위치 정보를 반영하기 위해 위치 정보를 담은 동일 크기의 행렬 Positional-Encoding Matrix 를 더하는 연산입니다.
Multi-Head Self-Attention & Add & Norm
다음은 핵심인 Multi-Head Self-Attention 에 대한 설명입니다.
Multi-Head Self-Attention 은 Self-Attention 을 Head 갯수만큼 병렬 실행하기 때문에 Multi-Head 라는 prefix 가 붙습니다.
Head 마다 Attention Value 를 만들고, 각 결과를 Concatenate 합니다.
Self-Attention (at 1 Head)
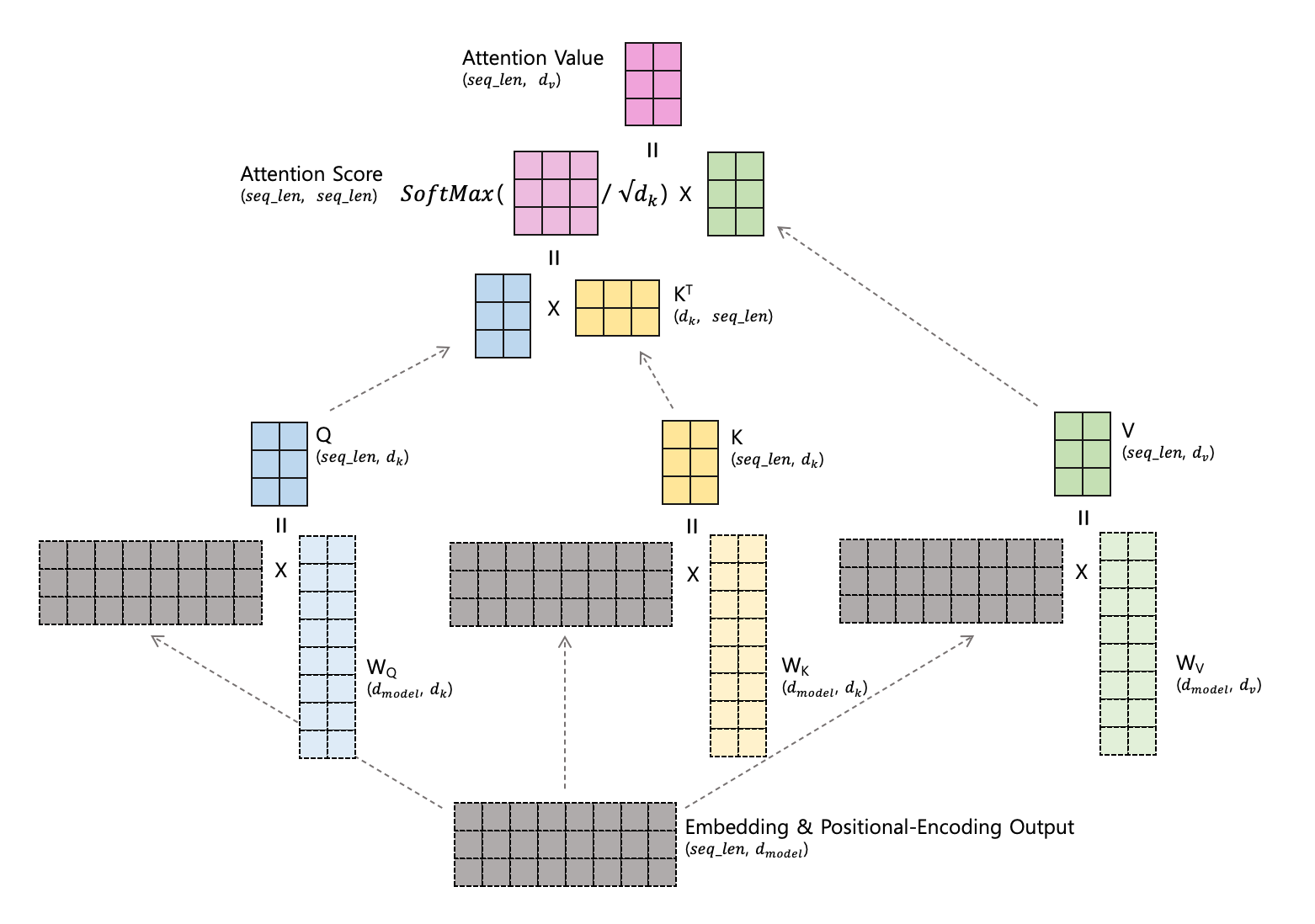
우선은 Head 하나에서 Self-Attention 이 어떻게 이루어지는지 살펴봅시다
하나의 Head 에서는 Embedding & Positional-Encoding Output $(seq\_len, d_{model})$ 으로 $Q$, $K$, $V$ 행렬을 만듭니다.
$Q$ 와 $K$ 는 $(seq\_len, d_k)$ 형태입니다. 그래서 변환을 담당하는 $W_Q, W_K$ 의 모양은 $(d_{model}, d_k)$ 입니다.
$V$ 는 $(seq\_len, d_v)$ 형태입니다. 그래서 변환을 담당하는 $W_V$ 의 모양은 $(d_{model}, d_v)$ 입니다.
만들어진 $Q$, $K$ 를 Scaled dot-product Attention 하여 Attention Score 를 만듭니다.
$(seq\_len, seq\_len)$ 형태가 나오는데, 이는 각 토큰 간의 Attention 점수를 의미합니다.
그리고 이것을 $V$ 와 내적하면 Attention Value $(seq\_len, d_v)$가 나옵니다.
Attention Value 의 i 번째 행 벡터: Attention Score 의 i 번째 행 벡터의 각 element 와 $V$ 의 각 행 벡터와 가중합 되는 방식입니다.
Self-Attention (at Multi-Head) 및 Add&Norm
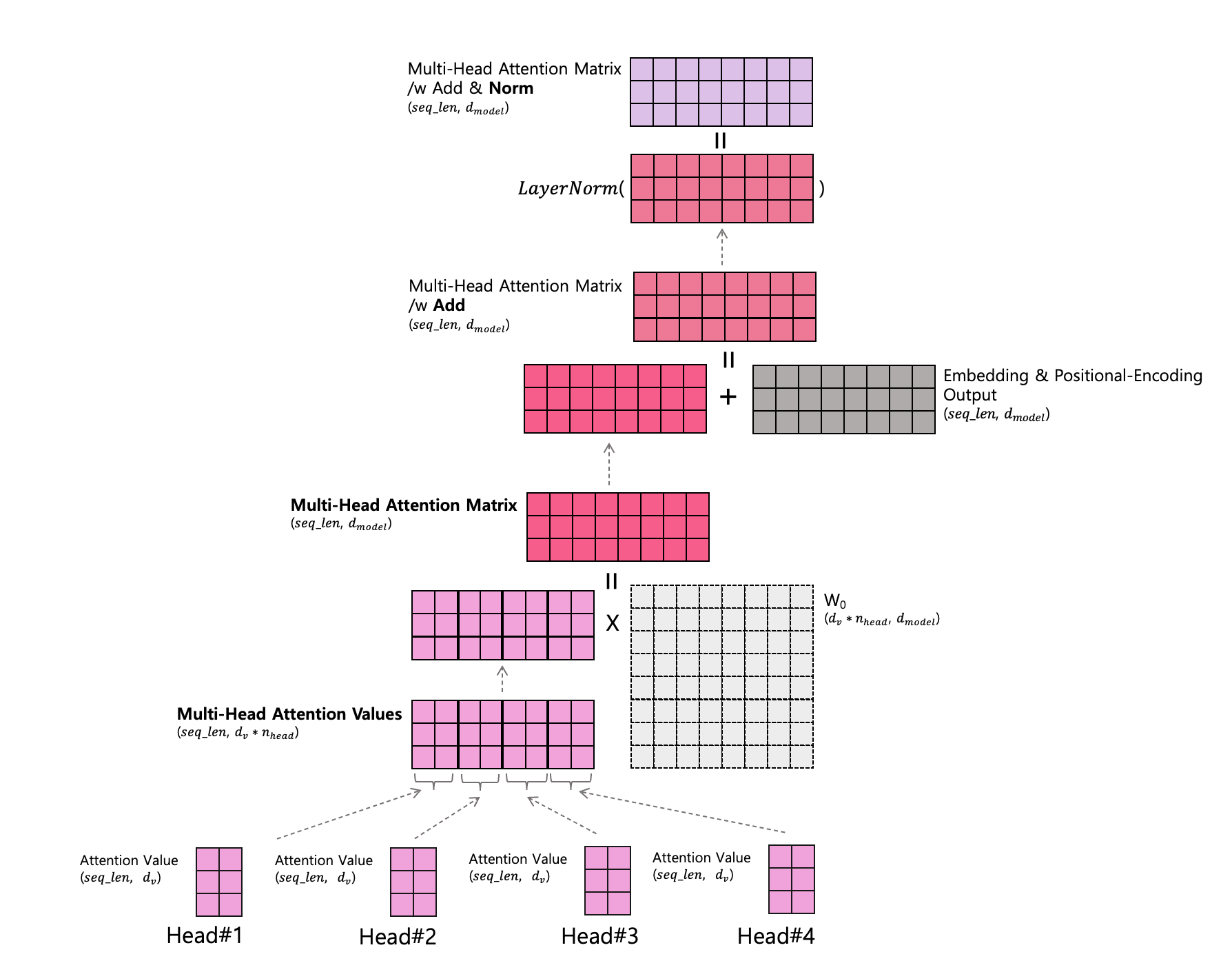
위에서는 하나의 Head 에서 처리되는 Self-Attention 에 대해 설명하였습니다.
여러 Heads 에서 각각 처리된 Attention Value $(seq\_len, d_v)$를 Concatenate 하면 Multi-Head Attention Values $(seq\_len, d_v * n_{head})$ 가 됩니다.
Multi-Head 를 사용하는 이유는 크게 두 가지입니다.
- 여러 관점에서 Attention 을 수행하여 다양한 정보를 얻기 위함
- 병렬 처리로 계산 속도를 향상하기 위함
이제 Multi-Head Attention Values $(seq\_len, d_v * n_{head})$ 을 Multi-Head Attention Matrix $(seq\_len, d_{model})$ 로 변환해야 하므로 $W_0$ 의 형태는 $(d_v * n_{head}, d_{model})$ 입니다.
그리고 그 윗쪽 층은 위에서 설명드린 Add&Norm (Residual Connection 과 Layer Normalization) 입니다.
- Residual Connection: Multi-Head Self Attention 층의 Output 인 Multi-Head Attention Matrix 과 Input 인 Embedding & Positional-Encoding Output 이 와 더해지는 구조입니다.
- Layer Normalization: 층 정규화를 거칩니다
Feed Forward Neural Network
Encoder 의 마지막 층입니다!
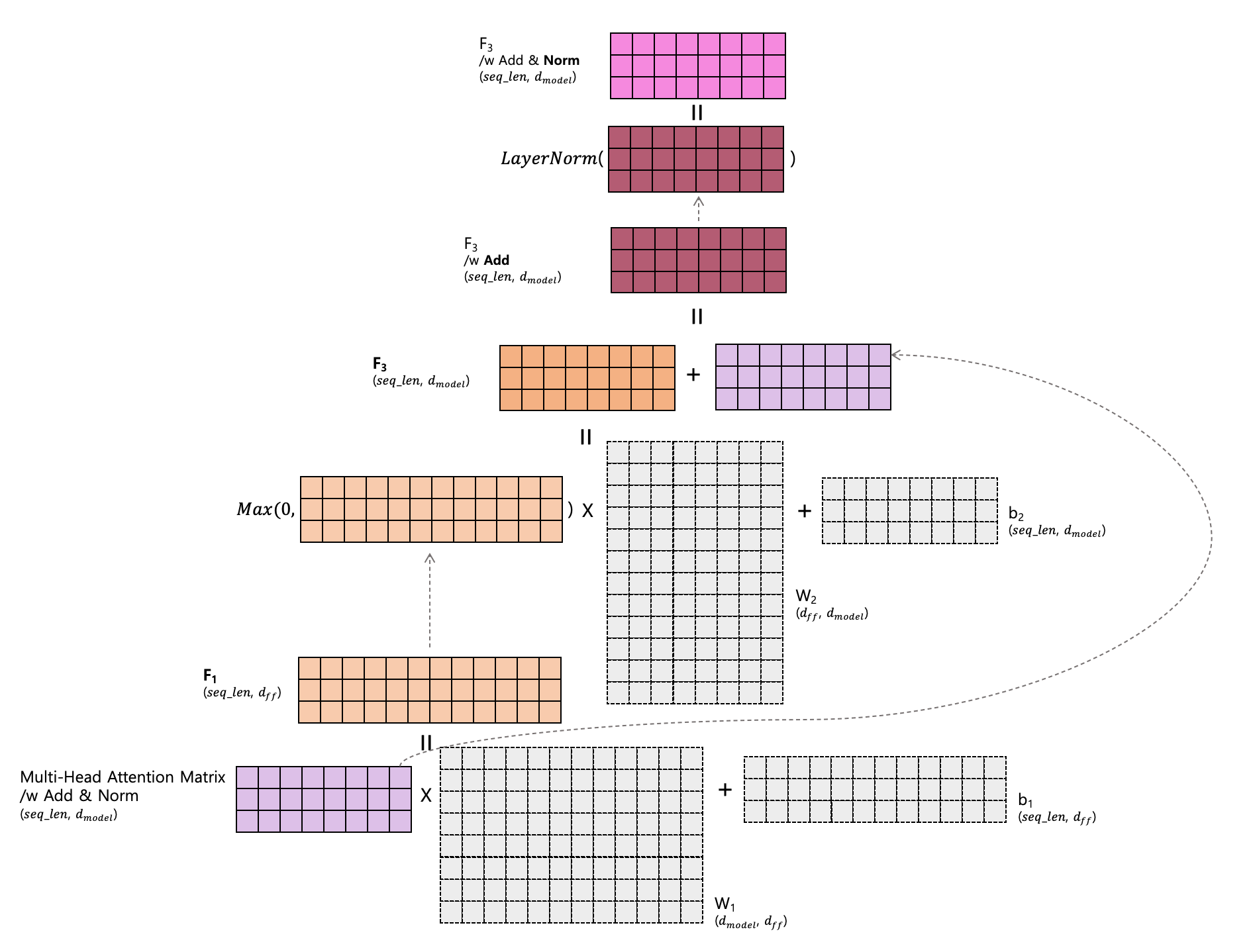
Feed Forward Neural Network 층입니다.
Multi-Head Self-Attention w/ Add&Norm $(seq\_len, d_{model})$ 을 $F_1 (seq\_len, d_{ff})$ 으로 변환하기 위해 $W_1 (d_{model}, d_{ff})$ 행렬이 사용됩니다. 그리고 $b_1 (seq\_len, d_ff)$은 bias 를 위한 행렬입니다.
그 후 ReLU 함수를 거치고 (Max(0, ...) 부분) 다시 $F_3 (seq\_len, d_{model})$ 형태로 변환하기 위해 $W_2 (d_{ff}, d_{model})$ 와 $b_1 (seq\_len, d_{model})$ 행렬이 사용됩니다.
그 후 위에서 설명드린 Add&Norm 층을 거치게 됩니다.
References
마치며
Transformer Encoder 에서 행렬 연산을 그림으로 이해해보았습니다.
글이 길어져 Decoder 는 다음 편에서 이야기 하겠습니다.
잘못된 부분이나 부족한 부분은 편하게 말씀해주시면 감사하겠습니다!
▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼
'머신러닝' 카테고리의 다른 글
| 하나의 예측값만 나오는 문제(Tree 모델) (1) | 2022.03.16 |
|---|---|
| [1탄] 딥러닝 음성 인식 - 자연신호의 디지털화 (2) | 2020.09.01 |
| [2탄] 딥러닝 음성 인식 - 디지털 신호의 특징 추출 (3) | 2020.09.01 |


