| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 선형대수
- simple linear regression
- 크롤링
- rct
- 인과 추론
- confounder
- 회귀불연속설계
- 교란변수
- 단순선형회귀
- 예제
- Omitted Variable Bias
- HTML
- least square estimation
- 잔차의 성질
- Instrumental Variable
- OVB
- 누락편의
- 최소제곱법
- causal inference
- 교란 변수
- 인과추론
- Sharp RD
- 네이버 뉴스
- residuals
- backdoor adjustment
- 사영
- Python
- LU분해
- 통계
- 머신러닝
- Today
- Total
Always awake,
[1탄] 딥러닝 음성 인식 - 자연신호의 디지털화 본문
"딥러닝을 이용한 음성인식(STT) 설명에 관한 포스팅입니다."
2019년도 여름에 국비교육으로 음성 지능에 관한 강의를 듣게 되었습니다.
기존에 다루던 스프레드시트 형식의 데이터와 다른 형태의 신호 데이터를 처리하고 모델링하는 것을 보면서 전기전자 분야의 신호처리 이론이 많이 적용되는 것을 느꼈습니다.
제가 이해한 내용을 바탕으로 본 포스팅을 작성하려 합니다.
1탄에서는 음성 신호에 관한 이론과 디지털 신호로 처리하는 방법을 설명하고
2탄에서는 디지털화 한 신호에서 특징을 추출하는 방법을 설명하겠습니다.
마지막으로 3탄에서는 이를 딥러닝 모델에 적용하여 STT(Speech To Text) 모델을 만드는 법을 공유하겠습니다.
본 포스팅을 준비하며 부족하거나 추가 자료가 필요한 부분은
유투브의 "김도현 대림대교수" 채널의 "디지털 오디오 기초이론 - Sample Rate/ Nyquist / Aliasing Freq." 영상을 참고하였습니다.
https://www.youtube.com/watch?v=aY42-xCsoRE
음성인식의 정의
음성인식(ASR)은 사람의 발성에 대한 음성 신호를 문자로 변환하는 기술입니다.
* ASR : Automatic Speech Recognition
- input : 사람의 발성이 담긴 신호(sequence)
- 음성 : 자연적 신호(continuous)
- 음성 디지털 신호 : 음성을 정해진 Hz에 따라 sampling 한 voltage 값
- process : 음성 인식 모델
- output : 음성에 해당하는 단어나 문장(sequence)
전체 프로세스와 고려할 사항은 다음과 같습니다.

본 포스팅에서는 위 그림에서 자연 음성 신호를 디지털 신호로 변환하는 단계까지 설명합니다.
자연신호와 음성신호
자연에서 발생하는 신호는 연속적인 파형으로 표현됩니다.
이 파형은 압축(+)과 팽창(-)을 반복하는 주기 함수로 표현됩니다.
one cycle
- 압축과 팽창으로 이루어짐
- 파장 : 각 peak까지 걸리는 시간의, 한 cycle이 경과하는데 걸리는 시간
- 주파수(frequency) : 얼마나 cycle이 빠르게 반복되는지에 대한 값, 파장의 역수
- 주파수가 높은 신호일수록 고음이 됩니다.
- 일반적으로 Hz(헤르츠)를 단위로 사용합니다.
※ Hz : 진동 수(cycle) / 1초

출처 : https://www.youtube.com/watch?v=aY42-xCsoRE
그리고 우리가 발화할 때 발생하는 음성 신호는 여러 주파수 신호의 합으로 표현됩니다
주파수 별로 압축, 팽창을 반복하는 주기적인 신호가 있고 이 신호들이 모두 합쳐져 음성 신호가 되는 것입니다.
- 음성 신호는 여러 주파수의 신호 합으로 표현

출처 : https://darkpgmr.tistory.com/171
디지털 신호처리
자연 신호를 디지털화 할 때 trade-off 문제
그렇다면 우리는 자연 신호를 어떻게 저장해야 할까요?
자연 신호(continuous) → 디지털 신호(discrete)로 변환할 때 발생하는 정보 손실을 최소화하여야 할 것입니다.
디지털화한 신호를 바탕으로 실제 자연 신호를 잘 추론할 수 있어야 합니다.
가장 좋은 방법은 신호의 값을 추출하는 sampling 기간을 짧게 하여 많은 양의 sample을 저장하는 것입니다. (sampling rate를 높입니다)
※ sampling rate : sample 수 / 1초
여기서 sampling rate를 높이면 자연 신호의 정보는 많이 유지되지만 저장 용량이 커지게 됩니다.
즉, 정보 보존과 저장 용량 이 두 가지 사이의 trade off 문제가 발생하게 됩니다.
※ HDD, SDD 등 메모리 및 저장 공간에 대한 비용이 저렴한 요즘과 달리
디스크나 CD를 사용했던 1970년대에는 저장 용량을 최소화하는 것이 매우 중요하였습니다.
나이퀴스트 이론(Nyquist Theory)
자연 음성 신호를 디지털화할 때
어느 정도의 sampling rate를 취해야 정보를 잘 보존하면서 저장 용량을 줄일 수 있을까 라는 의문에서 등장한 이론이
바로 나이퀴스트(Nyquist) 이론입니다.
나이퀴스트 이론은 sampling rate의 절반에 해당하는 주파수 대역까지 복원 가능하다는 이론입니다.
위에서 설명하였듯이 자연 신호는 하나의 cycle이 반복되는 파형입니다.
즉, 하나의 cycle을 알 수 있다면 해당 파형을 알 수 있습니다.
그렇다면 하나의 cycle을 알기 위해서는 sampling을 몇 번 진행하여야 할까요?
그림에서 보시는 것과 같이 위, 아래 peak를 알 수 있다면 한 cycle을 추론할 수 있을 것입니다.
그리고 이때의 sampling rate가 해당 신호의 주파수(frequency)의 2배가 됩니다.
적어도 이 두 peak를 알아야 continuous한 원 신호를 추론(복원)할 수 있습니다.

출처 : https://www.youtube.com/watch?v=aY42-xCsoRE
즉, 신호의 주파수의 최소 2배만큼 sampling rate를 설정해야 신호의 정보를 담을 수 있다는 의미입니다.
- 예시) 어떤 신호에서 8kHz의 주파수까지 담고 싶을 때 우리는 최소 sampling rate를 16kHz로 설정해야 합니다. (1초에 16000개의 sample 추출)
phase가 다른 경우
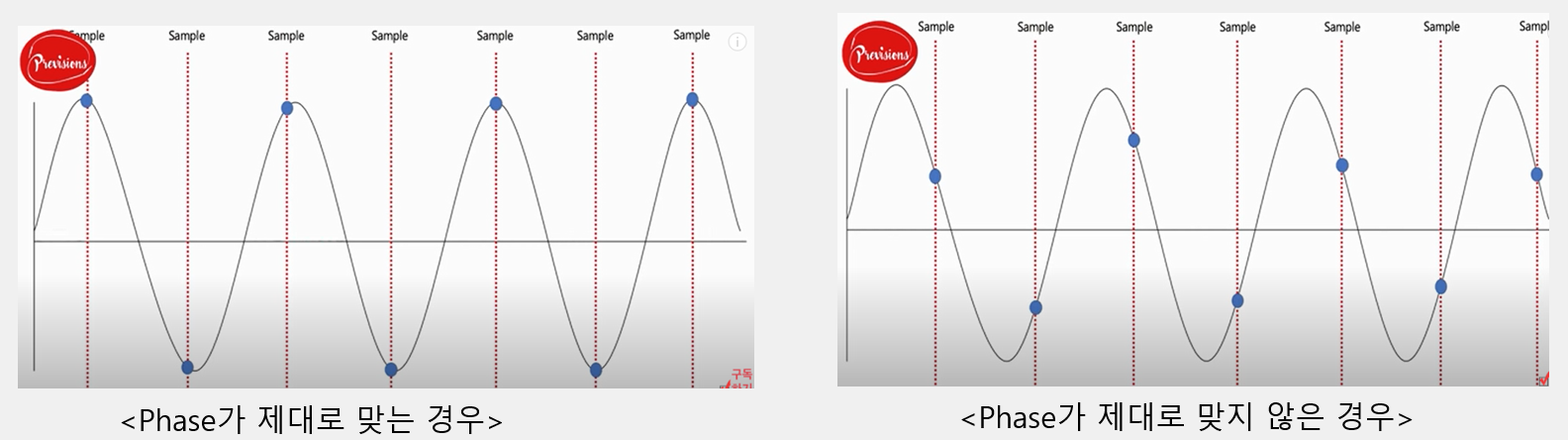
하지만 타이밍(phase)을 놓치는 경우 제대로 된 신호를 담지 못하게 됩니다.
출처 : https://www.youtube.com/watch?v=aY42-xCsoRE
같은 신호에 같은 sampling rate를 취하여 sampling 하였음에도
- 왼쪽 : peak를 잘 잡아냄. 원 신호 추론이 정확
- 오른쪽 : peak를 잡아내지 못함. 원 신호 추론이 부정확
와 같은 결과가 나타납니다.
이는 신호가 시작하는 시점(phase)이 다르기 때문에 나타나는 현상입니다.
Ghost Frequency(Aliasing Frequency)
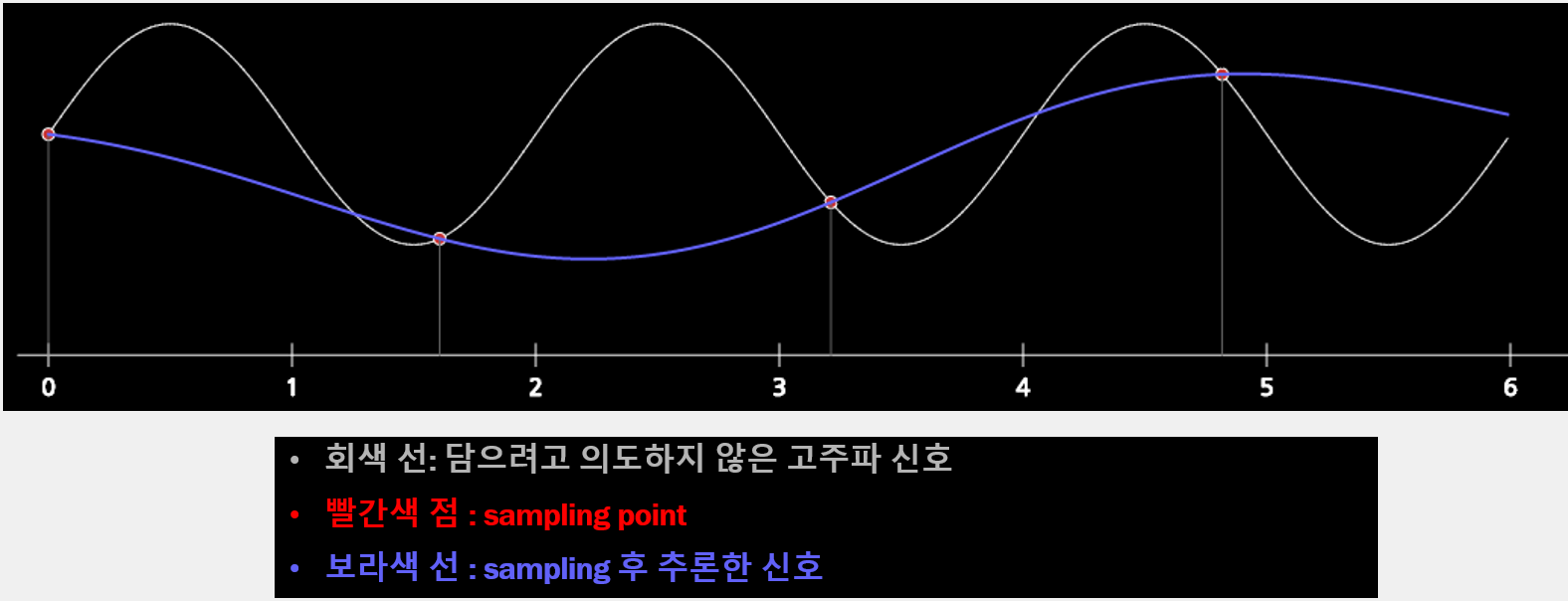
공기 중에는 다양한 주파수 대의 신호가 섞여있습니다. (특히, 고주파 대역)
그렇기 때문에 담으려고 의도하지 않은 공기 중의 고주파 신호는 디지털화 시 낮은 주파수로 표현될 수 있습니다.
이를 Ghost Frequency라고 합니다.
▶ 해결방안
해결방안은 허용 주파수 이외에는 잘라내는 방법입니다. 이를 Anti Aliasing Filter라고 합니다.
하지만, 22,050Hz까지의 slope이 남게 되기 때문에 sampling rate를 44.1kHz ( 22,050Hz * 2 )로 설정하는 것이 일반적입니다.

출처 : https://www.youtube.com/watch?v=aY42-xCsoRE
마치며
다음 포스팅(2탄)에서는 저장한 디지털 신호로 음성의 특징을 추출하는 방법에 대해 이야기하겠습니다.
긴 글 읽어주셔서 감사합니다.
피드백은 언제나 감사합니다~
▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼
'머신러닝' 카테고리의 다른 글
| Transformer 행렬 연산 #1 Encoder (0) | 2025.03.11 |
|---|---|
| 하나의 예측값만 나오는 문제(Tree 모델) (1) | 2022.03.16 |
| [2탄] 딥러닝 음성 인식 - 디지털 신호의 특징 추출 (3) | 2020.09.01 |


