| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 머신러닝
- 최소제곱법
- 교란변수
- residuals
- 회귀불연속설계
- Sharp RD
- 교란 변수
- causal inference
- HTML
- 잔차의 성질
- OVB
- rct
- 인과추론
- LU분해
- backdoor adjustment
- 단순선형회귀
- 네이버 뉴스
- Python
- 통계
- confounder
- Omitted Variable Bias
- 선형대수
- 예제
- 크롤링
- Instrumental Variable
- simple linear regression
- 사영
- 인과 추론
- 누락편의
- least square estimation
- Today
- Total
Always awake,
공분산과 상관계수 본문
"본 포스팅은 공분산과 상관계수를 개념적으로 이해하고, 수식을 통해 증명하기 위한 포스팅입니다"
확률과 통계학에서 회귀 모델이나 검정 시 공분산을 자주 접하게 됩니다.
두 변수의 선형적 상관성의 정도를 나타낸다는 설명이 수식을 접하면 잘 와닿지 않습니다.
그래서 간단한 기하학적 의미를 소개하고 이해하기 위한 포스팅을 준비해보았습니다.
공분산이란?(Covariance)
공분산은 두 확률 변수의 선형적인 상관성의 정도를 나타내는 값입니다.
확률변수 $X$, $Y$의 공분산 수식은 다음과 같습니다
$$
\begin{align*}
Cov(X,Y) &= E[ (X-E(X)) (Y-E(Y)) ] \\
&= E(XY) - E(X) E(Y)
\end{align*}
$$
어디서 많이 본 것 같지 않나요? 변수 자기 자신의 공분산은 자기 자신의 분산이 되는 것입니다.
$$Cov(X,X) = E(X^2) - (E(X))^2 = Var(X)$$
샘플링한 표본에 대한 공분산은 다음과 같습니다.
$$Cov(X,Y) = \large{ \frac{1}{n}\sum_{i=1}^n(x_i y_i) - \frac{1}{n} \sum_{i=1}^n(x_i ) \frac{1}{n} \sum_{i=1}^n(y_i )}$$
공분산의 기하학적 이해
공분산이 왜 두 변수의 선형적 상관성을 나타내는 것일까요?
수식을 해석하면 각 확률변수 $X$, $Y$ 의 자신의 평균($\bar{X}, \bar{Y}$) 과의 차이를 곱한 것의 기댓값입니다.
즉, 두 변수가 짝을 이루어 자신의 평균 대비 어느 방향으로 얼마나 떨어져 있는지 곱한 것의 기댓값입니다.
기하학적으로 설명해보겠습니다.
확률변수 $X$가 가로축, 확률변수 $Y$가 세로축이라면
해당 수식은 각 샘플에 대해 아래 그림에서 표현되는 사각형의 평균 넓이라고 할 수 있습니다.
(양의 상관성을 갖는 경우는 넓이 자체이고, 음의 상관성을 갖는 경우에는 넓이에 음의 부호를 적용한 것입니다)

즉, 두 변수가
- 양의 방향으로 선형적인 상관관계를 가진다면 공분산이 양의 값으로 커질 것이고
- 음의 방향으로 선형적인 상관관계를 가진다면 공분산은 음의 값으로 커질 것이며
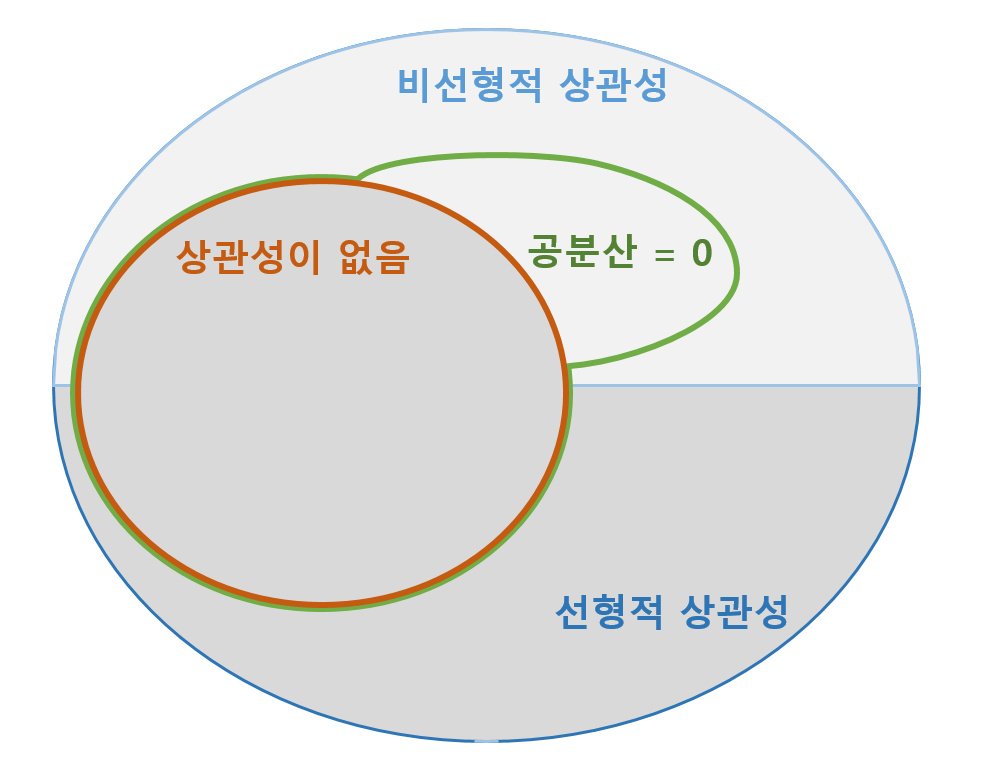
- 상관성이 없다면(두 변수가 서로 랜덤하게 분포한다면) 공분산은 0에 가까울 것입니다.
독립성과 공분산
두 변수가 독립이면 공분산은 0이 됩니다.
독립인 두 변수의 곱의 기댓값은 각 변수의 기댓값을 곱한 것과 같습니다.
$$E(XY) = E(X)E(Y)$$
따라서, 공분산의 수식에 의해 값이 0이 됩니다.
$$Cov(X,Y) = E(XY) - E(X) E(Y) = 0$$
두 확률변수가 독립이면 공분산의 값은 0이다
그렇다면 그 역도 성립할까요?
결론부터 말씀드리면 역은 성립하지 않습니다. (반례가 존재한다는 뜻입니다.)
공분산이 0이라는 것은 선형적으로 관계가 없다는 의미이기 때문입니다.
즉, 비선형적으로 관계가 있는 경우도 공분산 값이 0일 수 있습니다.
예시를 보겠습니다.
i.i.d 하게 균일 분포를 따르는 확률 변수 $X \sim Uniform(-1, 1)$ 가 있다고 합시다.
그리고 이 확률 변수 $X$ 비선형 관계를 갖는 $Y=X^2$ 가 있다고 합시다. 이 둘의 공분산 값은 무엇일까요?
공분산 수식 $Cov(X, Y) = E(XY) - E(X)E(Y)$ 에 $Y=X^2$ 를 넣으면 아래와 같이 됩니다.
$ Cov(X, Y) = Cov(X, X^2) = E(X^3) - E(X)E(X^2) $
한번 계산해보겠습니다. 우선 확률 변수 $X$ 의 확률밀도함수 $f(x)$ 는 아래와 같습니다
$ f(x) = \frac{1}{2} $
위에서 공분산 계산에 필요한 확률 변수 $X^3, X^2, X$ 의 각 기댓값을 구해보면
$
\begin{align*}
&E(X) = \int^{1}_{-1}{xf(x)}dx = \int^{1}_{-1}{\frac{1}{2}x}dx = \bigg[\frac{1}{4}x^2\bigg]^{1}_{-1} = 0
\\ &E(X^2) = \int^{1}_{-1}{x^2f(x)}dx = \int^{1}_{-1}{\frac{1}{2}x^2}dx = \bigg[\frac{1}{6}x^3\bigg]^{1}_{-1} = \frac{1}{2}
\\ &E(X^3) = \int^{1}_{-1}{x^3f(x)}dx = \int^{1}_{-1}{\frac{1}{2}x^3}dx = \bigg[\frac{1}{8}x^4\bigg]^{1}_{-1} = 0
\end{align*}
$
이를 대입하여 공분산 값을 구하면 0이 됩니다.
$Cov(X, Y) = Cov(X, X^2) = E(X^3) - E(X)E(X^2) = 0$
위와 같이 두 변수가 독립이 아닌 관계가 있는 경우에도 공분산의 값이 0 일 수 있습니다.
정리하면
- 두 변수가 독립이면 → 두 변수의 공분산의 값은 0
- 두 변수의 공분산의 값이 $\nrightarrow$ 두 변수는 독립
상관계수(Correlation)
상관계수의 필요성
공분산의 값이 크면 두 변수가 선형적인 상관성이 있다고 판단할 수 있을까요?
상황에 따라 다르지만 함부로 그렇다고 판단할 수 없습니다.
그 이유는 상관성이 있다/없다라는 판단을 하기 위해 기준 값이 필요하기 때문입니다.
예시를 들어보겠습니다.
변수 $X, Y$ 와 $A, B$가 있습니다.
둘은 2차원 평면에 점을 찍으면 다음과 같습니다.
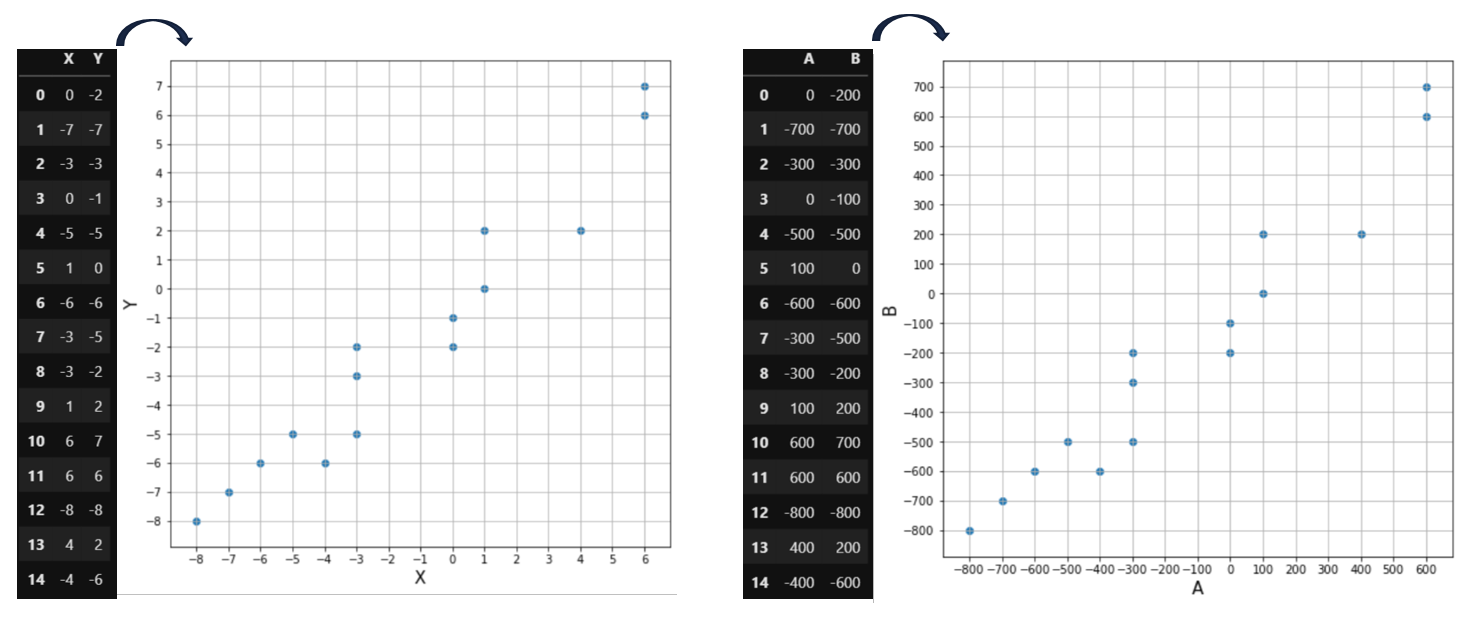
각 공분산을 구하면 다음과 같습니다.
$Cov(X,Y) = 19.77$
$Cov(A,B) = 197714.29$
공분산이 높기 때문에 "$A,B$의 상관성이 $X,Y$보다 크다" 라고 결론 짓는다면 이것은 잘못된 판단입니다.
왜냐하면 plot에서 보이는 것과 같이 $A, B$의 상관성과 $X, Y$의 상관성은 같기 때문입니다.
(사실 $A = 100X, B = 100Y$ 입니다)
즉, 변수의 크기나 범위만 달라졌을 뿐 두 변수의 상관성이 같기 때문에 공분산의 크기만으로 두 변수의 상관성을 판단하는 것은 자칫하면 큰 오류를 범할 수 있습니다.
이를 해결하기 위해 변수의 범위를 표준화하여 공분산을 구해야합니다.
이것이 바로 상관계수(Correlation)입니다.
상관계수는 표준화한 두 변수의 공분산 값이다.
상관계수(Correlation)의 수식은 다음과 같습니다.
$$
Corr(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)} \sqrt{Var(Y)}}
$$
표준화한다는 것은 아래의 식과 같이 변수를 평균으로 뺀 후 표준편차로 나누는 것입니다.
- $X' = \frac{X - E(X)}{\sqrt{Var(X)}}$
- $Y' = \frac{Y - E(Y)}{\sqrt{Var(Y)}}$
- $E(X') = 0, Var(X') = 1$
- $E(Y') = 0, Var(Y') = 1$
상관계수를 전개하면
$$
Corr(X, Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)} \sqrt{Var(Y)}} = \frac{E[(X-E(X)) (Y-E(Y))]}{\sqrt{Var(X)} \sqrt{Var(Y)}} = E\bigg[ \frac{X - E(X)}{\sqrt{Var(X)}} \frac{Y - E(Y)}{\sqrt{Var(Y)}} \bigg] = E[X'Y']
$$
이는 아래와 같이 다시 전개할 수 있습니다. $E(X') E(Y') = 0$ 임을 활용하여 $Cov(X', Y')$를 도출합니다.
$$
E(X'Y') = E(X'Y') - 0 = E(X'Y') - E(X') E(Y') = Cov(X', Y')
$$
즉, 아래의 식이 성립합니다.
$$
Corr(X, Y) = Cov(X', Y')
$$
상관계수는 두 변수를 스케일링 한 후 (평균을 0 으로, 분산을 1로 만들고) 공분산을 구한 것입니다. 표준화 효과를 가지게 됩니다.
두 변수의 스케일이나 범위에 상관 없이 상관성을 판단할 수 있는 표준화된 범위를 갖게 되는 것입니다.
위의 예시 데이터에서 상관계수를 구하면
$Corr(X,Y) = 0.97, Corr(A,B) = 0.97$ 로 같게 나오는 것을 볼 수 있습니다.
상관계수의 범위
그렇다면 표준화된 공분산인 상관계수의 범위는 어떻게 될까요?
결론부터 말씀드리면 상관계수의 범위는 $[-1,1]$입니다.
증명하면 다음과 같습니다.
확률 변수 $X'$과 $Y'$이 아래와 같을 때
- $X' = \frac{X - E(X)}{\sqrt{Var(X)}}$
- $Y' = \frac{Y - E(Y)}{\sqrt{Var(Y)}}$
- $E(X') = 0, Var(X') = 1$
- $E(Y') = 0, Var(Y') = 1$
$$
\begin{align*}
Var(X' + Y') &= Var(X') + Var('Y) + 2Cov(X',Y') \\
&= Var(X') + Var(Y') + 2Corr(X,Y) \\
&= 2 + 2Corr(X,Y)
\end{align*}
$$
분산은 항상 0보다 크므로 $Var(X' + Y') \geq 0$ 이고 따라서 $2 + 2Corr(X,Y) \geq 0$ 입니다.
그러므로 $Corr(X,Y) \geq -1$ 입니다.
마찬가지로 아래와 같이 동일한 논리를 적용하면
$$Var(X' - Y') = Var(X') + Var('Y) - 2Cov(X',Y') ...$$
$Corr(X,Y) \leq 1$ 입니다.
즉, 상관계수의 범위는 $[-1,1]$ 입니다.
두 변수가 선형적으로 증감 방향이 같은 경우: 상관계수 = 1
두 변수가 선형적으로 증감 방향이 다른 경우: 상관계수 = -1
두 변수가 독립인 경우: 상관계수 = 0 이 됩니다.
마치며
적으면서 수식이 정리되는 것 같아서 좋았습니다.
피드백 해주시면 감사하겠습니다 :)
▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼
'통계' 카테고리의 다른 글
| 신뢰성 분석 (1) | 2021.10.11 |
|---|---|
| 로지스틱 회귀(Logistic Regression) (3) | 2021.10.10 |
| 주성분 분석(PCA)의 개념적 이해 (0) | 2020.09.01 |
| 최대 우도 추정법(Maximum Likelihood Estimation) (6) | 2020.09.01 |
| 카이제곱 분포 모양 확인하기 (1) | 2020.08.30 |




