| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 최소제곱법
- 크롤링
- 회귀불연속설계
- Omitted Variable Bias
- Python
- causal inference
- Sharp RD
- 잔차의 성질
- residuals
- least square estimation
- 누락편의
- 통계
- 사영
- 머신러닝
- confounder
- 네이버 뉴스
- OVB
- 인과추론
- 선형대수
- 인과 추론
- Instrumental Variable
- 예제
- simple linear regression
- 단순선형회귀
- backdoor adjustment
- rct
- HTML
- 교란변수
- 교란 변수
- LU분해
- Today
- Total
Always awake,
로지스틱 회귀(Logistic Regression) 본문
로지스틱 회귀에 대한 개념, 수식 관련 포스팅입니다 :)
통계수업에서 가장 먼저 배우는 회귀 모델은 단순 선형 회귀(Simple Linear Regression)입니다.
- 종속변수와 독립변수가 각각 하나씩 존재하고,
- 독립변수와 종속변수의 관계가 선형인 회귀 모델입니다.
해당 모델은 종속변수가 실수값을 가지는 형태이고 가장 기초적인 모델이지만, 머신러닝을 배우면서 분류(Classification)문제를 접하게되면 해당 모델을 사용할 수 없게 됩니다.
그 이유는 분류 모델에서 종속변수는 하나의 class를 나타내는 "범주형" 변수이기 때문입니다. 즉, 실수형 변수와 다르게 값의 크기와 방향이 존재하지 않는 변수인 것입니다.
이런 문제로 탄생한 분류 모델이 로지스틱 회귀(Logistic Regression)입니다.
로지스틱 회귀는 클래스의 수가 2개(0 과 1) 이진 분류에 사용됩니다.
로지스틱 회귀의 컨셉
기존에 사용하던 선형 회귀를 분류 문제에 적용하려면 어떻게 해야할까요?
그 방법은 종속변수를 class로 배정할 수 있는 확률로 정의하는 것입니다. 종속변수에 변화를 주는 것이죠.
로지스틱 회귀의 컨셉은 다음과 같습니다.
단순 선형 회귀 모델 $y = \beta x$ 의 종속변수를 Link Function로 변환시키자!
* link function($y$) = $\beta x$
해당 컨셉을 만족하기 위해 종속변수가 다음과 같은 변화를 거치게 됩니다.
독립변수가 포함된 항(우항)은 그대로 사용할 것이므로 우리가 link function을 통해 변화시킨 종속변수(좌항)은 우항과 범위가 같아야 합니다.
우항의 범위는 (-∞, ∞) 이고 좌항을 이 범위에 맞추기 위해 적절한 변환을 할 수 있는 link function 을 찾는 것이죠!
STEP 1) 종속변수를 class 1(범주형)에 속할 확률로 정의하자 : $p$ ( 범위 : [0,1] )
이진 분류 문제이기 때문에 class는 0 또는 1 입니다.
class 1 에 속할 확률을 $p$ 로 정의하면 class 0 에 속할 확률은 $1-p$입니다. 확률 $p$를 기준으로 분류를 수행할 때 기준 값은 0.5(50%) 입니다.
- p ≥ 0.5 이면 class 1로 분류
- p < 0.5 이면 class 0으로 분류
하지만, 확률 $p$ 를 종속변수를 정의하면 우항의 범위와 맞지 않아서 사용할 수 없죠.
STEP 2) 클래스 0이 될 확률 대비 클래스 1이 될 확률의 비율(odds)로 정의하자 : $\large{\frac{p}{1-p}}$ ( 범위 : [0, ∞) )
여기서 odds란 "class1에 속할 확률 / class1에 속하지 않을 확률"입니다.
class 1에 속하지 않을 확률 대비 class 1에 속할 확률의 크기가 몇 배인지 나타내는 값입니다.
(이진 분류이므로 class1에 속하지 않을 확률 = class 0에 속할 확률)
따라서 class 분류 시 기준 값은 1 입니다.
- odds ≥ 1 이면 class1에 속할 확률이 그렇지 않은 확률보다 크거나 같으므로 class 1로 분류(p ≥ 0.5인 경우임)
- odds < 1 이면 class1에 속할 확률이 그렇지 않은 확률보다 작으므로 class 0으로 분류(p < 0.5인 경우임)
확률로 정의하였을 때보다는 범위가 넓어졌지만 이 역시도 우항과 범위가 맞지 않습니다.
STEP 3) 여기에 자연 로그를 씌워보자 : $ln(\large{\frac{p}{1-p}})$ ( 범위 : (-∞, ∞) )
위의 STEP 2에서 정의한 odds에 자연로그를 씌운 값입니다.
이제야 비로소 link function을 통해 변화시킨 좌항 값의 범위와 우항 값의 범위가 맞게 됩니다.
범주형 변수를 분류하는 문제를 확률로 다룰 수 있게 되고, 식의 좌항, 우항의 범위까지 맞게 됩니다!
우리는 이 link function을 logit function이라고 부릅니다(log + probit(=odds))
로지스틱 회귀에서의 확률
이제 식을 풀어서 좌항에 확률 $p$를 남겨봅시다.
그러면 아래와 같이 정리할 수 있습니다
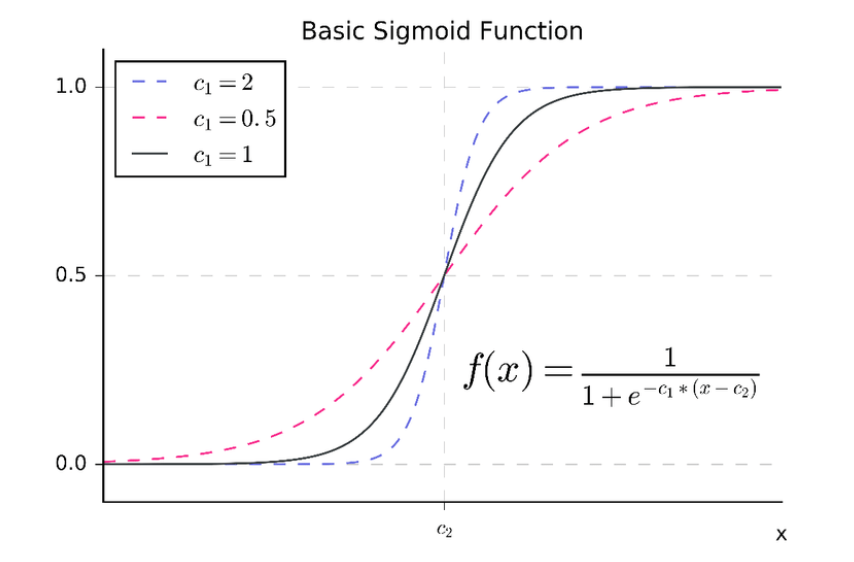
$$p = \frac{1}{1 + e^{- \beta x}}= sigmoid(\beta x)$$
즉, 기존에 사용한 회귀 모델에서 나온 독립변수항(우항)을 sigmoid 함수에 대입한 값이 1인 클래스에 속할 확률로서 정의됩니다.
해당 그래프에서 $c_1 = 1, c_2 = 0$인 것이 지금 설명하는 sigmoid function의 form입니다.
logit function 과 sigmoid function의 관계
위에서 정의한 것처럼 $logit(p) = \beta x$ 이고, $p = sigmoid(\beta x)$ 이므로 logit function과 sigmoid function은 서로 역함수 관계임을 알 수 있습니다.
- $logit(p) = \beta x$, $ln(\large{\frac{p}{1-p}})$ = $\beta x$
- $\Large{\frac{p}{1-p}}$ = $e^{\beta x}$
- $p = (1-p) e^{\beta x}$
- $p (e^{\beta x} + 1) = e^{\beta x}$
- $p = \Large\frac{e^{\beta x}}{e^{\beta x} + 1} = \frac{1}{1 + e^{- \beta x}}$ = $sigmoid(\beta x)$
확률($p$), 오즈, 로그 오즈의 관계
확률 $p$는 class 1에 속할 확률이므로 경계 값은 0.5(50%)입니다.
- 0.5 초과인 경우, class 1
- 0.5 미만인 경우, class 0
오즈는 class 0에 속할 확률 대비 class 1에 속할 확률의 비 이므로 경계 값은 1 입니다.
- 1 초과인 경우, class 1
- 1 미만인 경우, class 0
로그 오즈는 ($ln$(class 0에 속할 확률 대비 class 1에 속할 확률의 비))이므로 경계 값은 0 입니다.
- 0 초과인 경우, class 1
- 0 미만인 경우, class 0
로지스틱 회귀의 회귀 계수 해석
로그 오즈비
로지스틱 회귀에서의 회귀 계수 $\beta$는 로그 오즈비를 의미합니다. ( $odds = \frac{p}{1-p}$ )
$$ln(odds) = \beta x$$
$\beta$ 의 정체를 알기 위해 $x$가 1 단위 증가시켜 증가시키기 전과 비교해 봅시다.
증가 전과 후의 각 odds를 $odds_{b}, odds_{a}$ 라고 하겠습니다.
① 1 단위 증가 전: $ ln(odds_{b}) = \beta x $
② 1 단위 증가 후: $ ln(odds_{a}) = \beta (x + 1) $
② - ①: $ ln(\frac{odds_{a}}{odds_{b}}) = \beta$
즉, 회귀계수 $\beta$ 는 $x$ 1 단위 증가 전 대비 증가 후의 오즈비율의 로그 값입니다. 이를 로그 오즈비라고 합니다.
오즈비
로그 오즈비는 해석이 어려우므로, 오즈비로 해석하곤 합니다. 자연 상수를 밑으로 취하여 좌항의 $ln$(자연로그)을 풀어줍니다
$$ \frac{odds_{a}}{odds_{b}} = e^{\beta} $$
즉, $ e^{\beta}$ 는 $x$ 1 단위 증가 전 대비 증가 후의 오즈비 입니다.
예를 들어 우리가 관심 있는 변수의 회귀 계수($\beta$)가 -2 라고 하면 해당 변수가 1단위 증가했을 때,
로그 오즈비는 $-2$만큼 증가(2만큼 감소)하고, 오즈비는 $e^{-2} = 0.135 $ 입니다.
이것이 의미하는 것은 무엇일까요?
오즈비는 $\frac{(변수가 1단위 증가 후 class1 에 속할 확률)}{(변수가 1단위 증가 전 class1 에 속할 확률)}$ 이라고 하였습니다.
오즈비가 0.135 라는 것은 변수가 1단위 증가함으로 인해 class1 에 속할 확률이 그 전보다 낮아졌다는 것을 의미합니다. 즉, 해당 변수가 증가함에 따라 class1에 속할 확률이 감소하는 것입니다.
한계 효과(marginal effect)
로지스틱 회귀는 해당 class에 속할 확률을 추정하고 이를 로그 오즈비, 오즈비로 해석합니다.
오즈비, 로그 오즈비의 경우 해석 시 직관적이지 않은 경우가 있기에 이를 다시 확률로 변환하여 해석하기도 합니다.
이를 한계 효과(marginal effect)라고 부르며, 확률에 대해 변수가 미치는 영향(미분값)을 통해 구합니다
즉, 해당 변수가 1 단위 증가함에 따라 class 1에 속할 확률($p$)이 어떻게 변하는지 측정한 것입니다.
$$p = sigmoid(e^{\beta x}) = \frac{1}{1 + e^{-\beta x}}$$
$i$번쨰 독립 변수에 대한 marginal effect를 구하는 경우 해당 변수를 $x_i$라고 하면
$$\frac{\partial{p}}{\partial{x_i}} = \frac{\partial}{\partial{x_i}} (\frac{1}{1 + e^{-\beta x}})$$
$$= -\frac{e^{-\beta x}}{(1 + e^{-\beta x})^2} (-\beta_i) = \frac{e^{\beta x}}{(1 + e^{\beta x})^2} (\beta_i)$$
다음과 같이 marginal effect를 계산할 수 있습니다. 더 직관적인 해석이 가능합니다!
마치며
로지스틱 컨셉, 회귀 계수의 해석 방법
marginal effect에 대해서 알아보았습니다.
피드백 있으시면 댓글 부탁드립니다! 감사합니다
▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼
'통계' 카테고리의 다른 글
| 조건부 확률과 기댓값 (0) | 2021.12.26 |
|---|---|
| 신뢰성 분석 (1) | 2021.10.11 |
| 공분산과 상관계수 (11) | 2020.09.20 |
| 주성분 분석(PCA)의 개념적 이해 (0) | 2020.09.01 |
| 최대 우도 추정법(Maximum Likelihood Estimation) (6) | 2020.09.01 |




