| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- LU분해
- 사영
- Instrumental Variable
- least square estimation
- HTML
- 교란 변수
- 선형대수
- 최소제곱법
- 머신러닝
- rct
- Sharp RD
- 잔차의 성질
- 누락편의
- Omitted Variable Bias
- 인과추론
- Python
- simple linear regression
- 네이버 뉴스
- 통계
- 인과 추론
- 단순선형회귀
- 교란변수
- 크롤링
- confounder
- backdoor adjustment
- causal inference
- OVB
- 예제
- residuals
- 회귀불연속설계
- Today
- Total
Always awake,
도구 변수(IV) 예제 본문
"본 포스팅은 도구 변수(IV, Instrumental Variable)을 활용한 인과 추론 예제에 관한 내용입니다"
도구 변수 관련 내용은 아래 링크를 참고해주시면 감사하겠습니다.
도구 변수(IV)
본 포스팅은 도구변수에 대해 공부한 내용을 정리한 글입니다 :) 참고 서적 : Joshua D. Angrist, Jorn-Steffen Pischke. (2018). 고수들의 계량경제학. 시그마프레스. p.98 ~ p.144 들어가며 일전에 causal diag..
everyday-tech.tistory.com
데이터 생성
아래와 같은 형태로 예제 데이터를 생성합니다.
- $T$ : 원인 변수
- $Y$ : 결과 변수
- $W$ : (관측하지 못한) 교란 변수
- $Z$ : 도구 변수
추정해야할 인과 효과는 $T$가 $Y$에 미치는 영향인 $7$입니다

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as sm
np.random.seed(777) # 동일한 결과를 위해 시드 설정
num = 500 # 데이터 수
W = np.random.normal(size = num) # 교란 변수
Z = np.random.normal(size = num) # 도구 변수
# T는 W와 Z의 영향을 받습니다.
T = 5.0*W + 4.0*Z + np.random.normal(size = num) # 원인 변수
# Y는 X와 W의 영향을 받습니다.
Y = 10.0*W + 7.0*T + np.random.normal(size = num) # 결과 변수
data = pd.DataFrame({'T' : T, 'W' : W, 'Y' : Y})
단순 비교
교란 요인 $W$를 통제하지 않은 상태에서 단순히 $T$와 $Y$의 관계를 비교하는 경우 정확한 인과 효과를 추정하지 못합니다
(추정값이 $8.1173$로 실제 인과 효과인 $7$과 매우 다름)
# 단순 비교
sod_model = sm.ols('Y ~ T', data).fit()
# 교란 변수를 누락하였기에 인과 효과가 잘못 추정됨
sod_model.summary().tables[1]
교란 요인 $W$의 영향을 제거한 후 $T$가 $Y$에 미치는 인과 효과를 추정하기 위해서는 교란 요인을 통제한 모델($Y ~ T + W$)에서의 $T$의 회귀 계수를 확인하면 됩니다.
하지만 교란 요인 $W$는 관찰되지 못한 상태이므로 교란 요인을 통제하는 방법으로 인과 효과를 추정할 수 없습니다.
이 때, 도구 변수를 활용하면 인과 효과를 추정할 수 있습니다.
도구 변수를 활용한 추정
도구 변수 $Z$는 교란 변수 $W$와 상관성이 없고, 원인 변수 $T$와 상관성이 매우 높기 때문에 이를 활용하여 인과 효과를 추정합니다.
절차는 다음과 같습니다.
- first stage model : $Z$가 $T$에 미치는 영향을 추정 ($\phi$)
- reduced model : $Z$가 $Y$에 미치는 영향을 추정 ($\rho$)
→ $T$가 $Y$에 미치는 인과 효과 : $\large{\frac{\rho}{\phi}}$
데이터를 통해 확인해보겠습니다
도구 변수를 사용한 인과 효과 추정
# first stage model(Z -> T)
stage1_model = sm.ols('T ~ Z', data).fit()
# reduced model(Z -> Y)
reduced_model = sm.ols('Y ~ Z', data).fit()first stage model
# first stage model
stage1_model.summary().tables[1]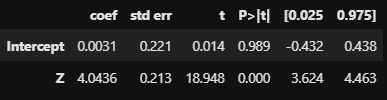
$\phi = 4.0436$
reduced model
# reduced model
reduced_model.summary().tables[1]
$\rho = 28.3041$
즉, 인과 효과 = $\large{\frac{\rho}{\phi}}$ = $28.3041/4.0436 = 6.9997$ 로 실제 인과 효과인 $7$을 잘 추정한 것을 알 수 있습니다.
도구 변수를 활용한 추정(2SLS)
위에서 알려드린 방법은 인과 효과의 평균 값만 확인한 것입니다.
따라서 인과 효과의 유의성, 신뢰구간을 확인하기 위해 first stage model에서 $\hat{T}$(예측된 $T$)을 $Y$에 회귀시키는 2SLS(Two Stage Least Square)를 사용합니다.
인과 효과는 위에서 계산한 값($6.9997$)과 동일합니다
# first stage
t_hat = stage1_model.predict()
data['T_hat'] = t_hat
# second stage
stage2_model = sm.ols('Y ~ T_hat', data).fit()# first stage model
stage2_model.summary().tables[1]
2SLS를 이용하여 추정한 인과 효과는 $6.9997$이며,
p-value가 매우 작으므로 인과 효과가 유의하다고 판단할 수 있습니다!
참고로, 위에서 계산한 추정값과 동일합니다
마치며
인과 추론 시 교란 변수를 누락 문제를 해결하기 위한 방법으로 도구 변수(IV)에 대해 설명하였으며
실제 계산 방법을 예제를 통해 알아보았습니다.
피드백은 댓글로 남겨주시면 감사하겠습니다!
▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼
'인과추론(Causal Inference)' 카테고리의 다른 글
| 불연속회귀설계(RDD) (0) | 2021.10.04 |
|---|---|
| 이중차분법(DID) (0) | 2021.10.02 |
| 도구 변수(IV) (2) | 2021.07.20 |
| 누락 편의(OVB) 예제 (3) | 2021.07.20 |
| 누락 편의(OVB) (0) | 2021.07.17 |




