| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- LU분해
- 인과 추론
- 네이버 뉴스
- 회귀불연속설계
- confounder
- Sharp RD
- 단순선형회귀
- 크롤링
- 잔차의 성질
- 누락편의
- 통계
- 인과추론
- HTML
- 교란 변수
- backdoor adjustment
- causal inference
- residuals
- rct
- 사영
- Omitted Variable Bias
- 예제
- least square estimation
- 선형대수
- 교란변수
- OVB
- Instrumental Variable
- 머신러닝
- Python
- simple linear regression
- 최소제곱법
- Today
- Total
Always awake,
누락 편의(OVB) 예제 본문
일전에 포스팅한 누락 편의(OVB)의 예제를 살펴보는 글입니다 :)
본 포스팅에서 사용하는 변수명 및 notation은 아래 내용과 이어지니 먼저 확인하고 오시면 좋습니다.
누락 편의(OVB)
누락 편의에 대해 공부한 내용을 정리한 글입니다 :) 참고 서적 : Joshua D. Angrist, Jorn-Steffen Pischke. (2018). 고수들의 계량경제학. 시그마프레스 p.90 ~ p.91 누락 편의 개념 누락 편의란 통제가 필요한..
everyday-tech.tistory.com
누락 편의 예제
일전 포스팅에서 누락 편의는 다음과 같이 계산된다고 말씀드렸습니다.
- (model1: $W$를 누락한 모델) $Y_i = \beta_0 + \beta_1 X_i + \epsilon_{1i}$
- (model2: $W$를 포함한 모델) $Y_i = \gamma_0 + \gamma_1 X_i + \gamma_2 W_i + \epsilon_{2i}$
- (model1_sub: model1의 독립항을 누락 변수에 회귀시킨 모델) $W_i = \pi_0 + \pi_1 X_i + \epsilon_{3i}$
누락 편의의 정의에 의해 $OVB = \beta_1 - \gamma_1$ 이고 $\pi_1 \gamma_2$로 계산 가능하다 하였습니다.
실제 예시를 통해 $OVB = \beta_1 - \gamma_1 = \pi_1 \gamma_2$이 성립하는지 확인해보겠습니다.
예제 Causal Diagram

$X$ : 원인 변수, $Y$ : 결과 변수, $W$ : 교란 변수일 때,
각 노드끼리 edge의 quantity만큼 서로 영향을 미칩니다.
이를 표현하기 위해 아래와 같이 데이터를 만들어줍니다(python 3.x 사용)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as sm
np.random.seed(777) # 동일한 결과를 위해 시드 설정
num = 500 # 데이터 수
W = np.random.normal(size = num)
# X는 W의 영향을 받습니다.
X = 4.0 * W + np.random.normal(size = num)
# Y는 X와 W의 영향을 받습니다.
Y = 8.0 * W + 14.0 * X + np.random.normal(size = num)
data = pd.DataFrame({'X' : X, 'W' : W, 'Y' : Y})
각 모델을 fitting 합니다.
# model1 : 누락 변수W를 누락한 모델
model1 = sm.ols('Y ~ X', data).fit()
# model2 : 누락 변수W를 포함한 모델
model2 = sm.ols('Y ~ X + W', data).fit()
# model1_sub : model1의 독립항을 누락 변수W에 회귀시킨 모델
model1_sub = sm.ols('W ~ X', data).fit()
이제 각 모델의 회귀 계수를 확인해봅니다.
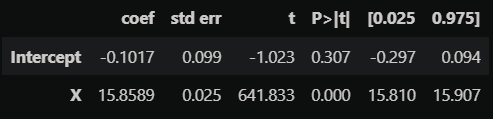
model1 : 누락 변수 $W$를 누락한 모델
$X$의 회귀 계수는 위에서 $\beta_1$을 의미합니다. 즉, $\beta_1 = 15.8589$ 로 추정됩니다.
model1.summary().tables[1]
model2 : 누락 변수 $W$를 포함시킨 모델
model2.summary().tables[1]

$X$의 회귀 계수는 위에서 $\gamma_1$을 의미하고, $W$의 회귀 계수는 $\gamma_2$를 의미합니다.
즉, $\gamma_1 = 14.0260$, $\gamma_2 = 7.8592$로 추정됩니다.
model1_sub : model1의 독립항을 누락 변수 $W$에 회귀시킨 모델
model1_sub.summary().tables[1]

$X$의 회귀 계수는 위에서 $\pi_1$을 의미합니다.
즉, $\pi_1 = 0.2332$ 입니다. ($X$가 $W$에 미치는 Association을 의미합니다.)
최종 확인
이제 최종적으로 위에서 제시한 OVB formula가 맞는지 확인해봅니다.($\beta_1 - \gamma_1 = \pi_1 \gamma_2$)
- (좌항) $\beta_1 - \gamma_1 = 15.8589 - 14.0260 = 1.8330$
- (우항) $\pi_1 \gamma_2 = 0.2332 * 7.8592 = 1.8330$
으로 계산 결과 일치하는 것을 알 수 있습니다.
(참고) 해석
참고로, 누락 편의를 해석하면 누락 변수 $W$를 모델에 포함하지 않음으로써 인과 효과가 1.8330만큼 과대 추정된다는 의미입니다.
만약 교란 변수 $W$가 $X$에 미치는 영향과 $Y$에 미치는 영향이 반대(반대 부호) 인 경우 OVB 값은 음수가 되고,
이런 경우에는 과소 추정하게 됩니다.
마치며
OVB를 계산하는 방법과 실제 예제로 확인해보았습니다.
혹시 잘못된 부분이 있다면 피드백 주시면 감사하겠습니다 :)
▼ 글이 도움이 되셨다면 아래 클릭 한번 부탁드립니다 :) ▼
'인과추론(Causal Inference)' 카테고리의 다른 글
| 도구 변수(IV) 예제 (0) | 2021.08.26 |
|---|---|
| 도구 변수(IV) (2) | 2021.07.20 |
| 누락 편의(OVB) (0) | 2021.07.17 |
| [인과 추론 발표] 2021 Summer Session On Causal Inference (0) | 2021.07.16 |
| backdoor adjustment (0) | 2021.07.12 |



