수치 미분을 해보자

 

 

본 포스팅은 수치 미분에 대해 공부하고 코드를 구현하며 나름대로 정리한 글입니다.

 

수치 미분(Numerical Difference) 란 미분의 근사치를 구하는 방법입니다.

미분 정의

함수 $f(x)$ 에 대한 $x$ 의 미분값은 특정 값에서의 순간 변화량(기울기) 로 표현됩니다. 함수 $f(x)$ 수식을 알고 있는 경우 미분 함수 $f'(x)$ 의 수식을 구할 수 있으니 미분 값을 구할 수 있습니다.

$$ f'(x) = lim_{\epsilon \rightarrow 0}\frac{f(x+\frac{\epsilon}{2}) - f(x-\frac{\epsilon}{2})}{\epsilon}$$

 

예를 들어 아래와 같은 함수가 있으면

$$f(x) = x^3 + x^2 + 1$$

1차 미분 함수는 아래와 같이 전개할 수 있습니다

$$\begin{align*}
f'(x) & = \frac{df(x)}{dx}
\\
&= lim_{\epsilon \rightarrow 0}\frac{f(x + \frac{\epsilon}{2}) - f(x - \frac{\epsilon}{2})}{\epsilon}
\\
& = lim_{\epsilon \rightarrow 0}\frac{[x^3 + 3x^2\frac{\epsilon}{2} + 3x(\frac{\epsilon}{2})^2 + (\frac{\epsilon}{2})^3 +  x^2 + \epsilon x + (\frac{\epsilon}{2})^2 + 1] - [x^3 - 3x^2\frac{\epsilon}{2} + 3x(\frac{\epsilon}{2})^2 - (\frac{\epsilon}{2})^3 + x^2 - \epsilon x + (\frac{\epsilon}{2})^2 + 1]}{\epsilon}
\\
& = lim_{\epsilon \rightarrow 0} \frac{3x^2\epsilon + \frac{\epsilon^3}{4} + 2\epsilon x}{\epsilon}
\\
& = lim_{\epsilon \rightarrow 0}{3x^2 + \frac{\epsilon^2}{4} + 2 x}
\\
& = 3x^2 + 2 x
\end{align*}$$

 

수치 미분이란?

하지만 컴퓨터로 이를 계산할 때는 미분 함수의 꼴을 알 수가 없기 때문에 미분 함수를 구하는 방식을 묘사하여 근사치를 구합니다. 여기서 묘사한다는 뜻은 $x$ 의 매우 작은 변화 $\epsilon$ (예를 들어 1e-05) 에 대한 $f(x)$ 의 변화량을 구해 미분값의 근사치를 구하는 것입니다. 

$$f'(x) = lim_{\epsilon \rightarrow 0}\frac{f(x + \frac{\epsilon}{2}) - f(x - \frac{\epsilon}{2})}{\epsilon} \approx \frac{f(x + \frac{\epsilon}{2}) - f(x - \frac{\epsilon}{2})}{\epsilon}$$

 

코드로 확인하기

위의 예시를 코드로 확인해봅니다

함수 정의

먼저 함수 $f(x)$ 와 1차, 2차 미분 함수($f'(x), f''(x)$) 를 정의해줍니다

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def f(x: float):
    return x**3 + x**2 + 1

def f_derivative1(x: float):  # f 1차 미분
    """First Order Derivative of Function `f`"""
    return 3*(x**2) + 2*x

def f_derivative2(x: float):  # f 2차 미분
    """Second Order Derivative of Function `f`"""
    return 6*x + 2

함수의 개형은 아래와 같습니다

x = np.linspace(-100, 100, num=1000)

f_x = f(x=x)
f_drv1_x = f_derivative1(x=x)
f_drv2_x = f_derivative2(x=x)
f_drv3_x = f_derivative3(x=x)

plt.plot(x, f_x,
        color="black", linewidth=4)
plt.xlabel("x")
plt.ylabel("y")
plt.title("y=f(x)")
plt.grid()
plt.show()

plt.plot(x, f_drv1_x,
        color="black", linewidth=4)
plt.xlabel("x")
plt.ylabel("y")
plt.title("y=f'(x)")
plt.grid()
plt.show()

plt.plot(x, f_drv2_x,
        color="black", linewidth=4)
plt.xlabel("x")
plt.ylabel("y")
plt.title("y=f''(x)")
plt.grid()
plt.show()

1차 미분 함수

2차 미분 함수

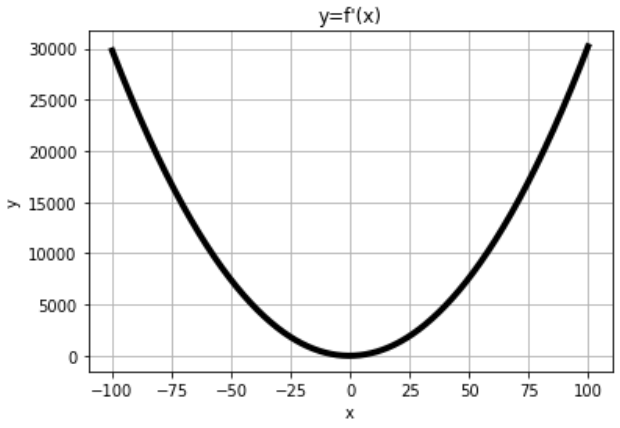
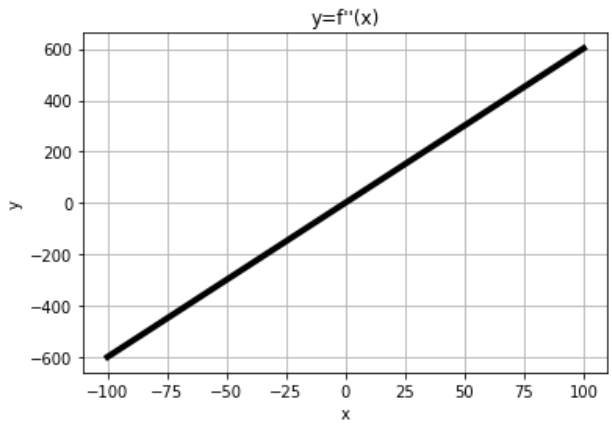
수치 미분(1차 미분)

이제 수치 미분을 활용하여 근사치를 구하고 위의 1차 미분 함수와 값이 일치하는지 확인해봅니다

def dydx(x: float, func: callable, eps: float = 1e-05):
    """Numerical First Order Deravative of function argument `func`"""
    x_b = x - eps/2
    x_a = x + eps/2
    
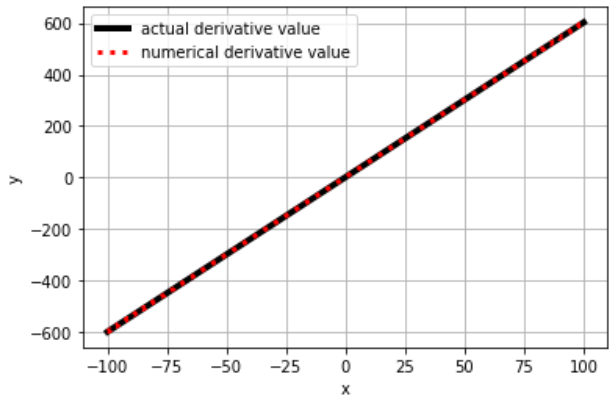
    return (func(x_a) - func(x_b)) / eps

검정색은 위에서 정의한 1차 미분 함수 개형이고, 빨간색은 1차 수치 미분 함수 개형입니다.

둘이 개형이 일치하는 것을 알 수 있습니다

dydx1_x = dydx(x=x, func=f)

plt.plot(x, f_drv1_x, 
         label="actual derivative value", linestyle="solid", color="black", linewidth=4)
plt.plot(x, dydx_x, 
         label="numerical derivative value", linestyle="dotted", color="red", linewidth=3)
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.legend()
plt.show()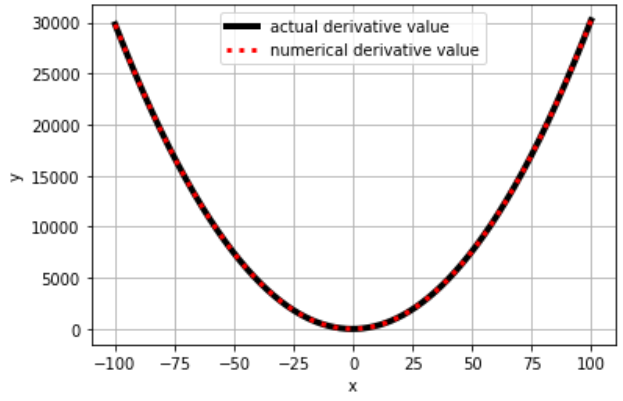

1차 미분 함수 값 vs. 1차 수치 미분 함수 값

단, 여기서 주의해야 할 것은 두 값이 완전히 일치하지 않는다는 것입니다. 말 그대로 근사치 이므로 아래와 같이 오차가 발생합니다.

np.abs(f_drv1_x - dydx_x).max()

오차가 발생합니다

수치 미분(n차 미분) 

위에서 만든 수치 미분 함수는 1차 미분 근사치만 계산할 수 있습니다. 그렇다면 2차 이상의 수치 미분은 어떻게 할까요? 

 

함수를 만들기 전에 먼저 2차 미분에 대한 수식을 살펴봅시다. 2차 미분 함수 $f''(x)$는 1차 미분 함수 $f'(x)$를 한번 더 미분한 것입니다.

$$\begin{align*}
f''(x) &= \frac{df'(x)}{dx}
\\
&= lim_{\epsilon \rightarrow 0}\frac{f'(x + \frac{\epsilon}{2}) - f'(x - \frac{\epsilon}{2})}{\epsilon}
\end{align*}$$

그래서 위와 같이 수치 미분을 이용하여 매우 작은 $\epsilon$ 을 이용하면 근사치를 구할 수 있습니다

$$\begin{align*}
f''(x) &= \frac{df'(x)}{dx}
\\
& = lim_{\epsilon \rightarrow 0}\frac{f'(x + \frac{\epsilon}{2}) - f'(x - \frac{\epsilon}{2})}{\epsilon}
\\  
& \approx \frac{f'(x + \frac{\epsilon}{2}) - f'(x - \frac{\epsilon}{2})}{\epsilon}
\\
& \approx \frac{\frac{f(x + \frac{\epsilon}{2}) - f(x - \frac{\epsilon}{2})}{\epsilon} - \frac{f(x + \frac{\epsilon}{2}) - f(x - \frac{\epsilon}{2})}{\epsilon}}{\epsilon}
\end{align*}$$

 

근사치 수식 (수치 미분) 꼴을 보면 뭔가 반복되는 느낌이 듭니다. n차 수치 미분 시에는 n-1 차 수치 미분 함수에 대해 수치 미분을 하는 것이지요.

위의 성질을 이용하면 2차 수치 미분 뿐만 아니라 3차 이상의 수치 미분을 할 수 있습니다. 일반화된 n차 수치 미분 함수를 만들 수 있는 것이지요 

 

이는 아래와 같이 재귀 함수를 이용하여 구현할 수 있습니다

order 가 주어지면(n차 미분에서 값 n) order-1 수치 미분 함수에 대해 수치 미분을 하는 꼴입니다. 이는 order 1이 될 때까지 수행되고 order 가 1일 때는 1차 수치 미분 값을 반환합니다

def dydx_order(x: float, func: callable, eps: float = 1e-05, order: int = 1):
    """Numerical `order` Deravative of function argument `func`"""
    x_b = x - eps/2
    x_a = x + eps/2
    
    if order == 1:
        return (func(x_a) - func(x_b)) / eps
    else:
        return (dydx_order(x_a, func=func, order=order-1) - dydx_order(x_b, func=func, order=order-1)) / eps

결과를 보면 위에서 정의한 미분 함수 값과 같은 개형을 띄는 것을 알 수 있습니다

검정색은 미분 함수의 개형이고, 빨간색은 수치 미분 함수 개형입니다

(단 위에서 언급한 것과 같이 오차가 발생함은 기억해야 합니다)

dydx1_x = dydx_order(x=x, func=f, order=1)
dydx2_x = dydx_order(x=x, func=f, order=2)

plt.plot(x, f_drv1_x, 
         label="actual derivative value", linestyle="solid", color="black", linewidth=4)
plt.plot(x, dydx1_x, 
         label="numerical derivative value", linestyle="dotted", color="red", linewidth=3)
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.legend()
plt.show()


plt.plot(x, f_drv2_x, 
         label="actual derivative value", linestyle="solid", color="black", linewidth=4)
plt.plot(x, dydx2_x, 
         label="numerical derivative value", linestyle="dotted", color="red", linewidth=3)
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.legend()
plt.show()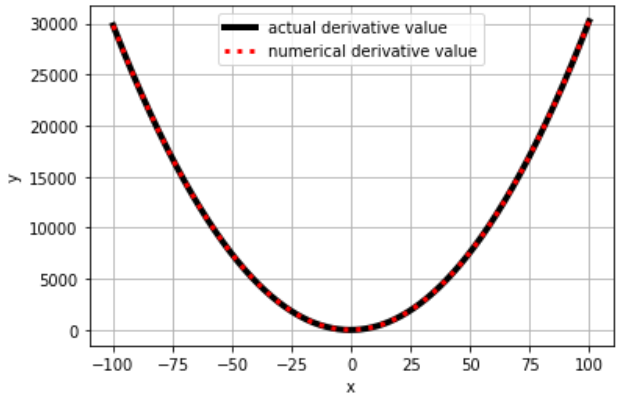

1차 미분 함수 값 vs. 1차 수치 미분 함수 값

2차 미분 값 vs. 2차 수치 미분 값

마치며

수치 미분 함수 및 구현에 대해 알아보았습니다. 

수식을 바탕으로 반복되는 꼴에 대해 탐색하고 이를 재귀함수로 구현해보는 좋은 경험이었습니다

포스트를 작성하다보니 수치 미분을 하면 오차가 발생할 수 밖에 없는데 이를 줄일 수 있는 방법은 어떤 것이 있는지 궁금해집니다. 이 부분도 시간이 나면 공부해봐야겠습니다 😊

 

긴 글 읽어주셔서 감사합니다. 피드백은 언제나 환영합니다!