| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Omitted Variable Bias
- 인과추론
- 네이버 뉴스
- HTML
- residuals
- LU분해
- 머신러닝
- OVB
- 잔차의 성질
- Sharp RD
- 회귀불연속설계
- backdoor adjustment
- 크롤링
- rct
- 통계
- least square estimation
- Python
- simple linear regression
- 교란변수
- 누락편의
- 선형대수
- 인과 추론
- 최소제곱법
- 교란 변수
- causal inference
- Instrumental Variable
- 예제
- 사영
- 단순선형회귀
- confounder
- Today
- Total
Always awake,
이중차분법(DID) 예제 본문
본 포스팅은 이중차분법을 활용한 인과 효과 측정 예제입니다 :)
이중차분법에 대한 내용은 아래의 포스팅을 참고하시면 좋습니다.
이중차분법(DID)
본 포스팅은 이중 차분법에 대해 공부한 내용을 정리한 글입니다 :) 참고 서적 : Joshua D. Angrist, Jorn-Steffen Pischke. (2018). 고수들의 계량경제학. 시그마프레스. p.178 ~ p.190 이중 차분법 컨셉 이중..
everyday-tech.tistory.com
예제 데이터를 생성하여 두 가지 방식으로 이중 차분 값(인과 효과)을 측정해보겠습니다.
예제 데이터 생성
총 10개의 time stamp에 대해 처치 그룹(treated group)과 통제 그룹(control group) 각각의 결과 변수(outcome)입니다
처치 그룹은 통제 그룹에 비해 8 높으며, 처치 시점 이후 인과 효과에 의해 13이 더 높아집니다
여기서 우리가 구하고자 하는 인과 효과는 13 입니다
# 패키지 import
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as smnp.random.seed(777) # 동일한 결과를 위해 시드 설정
treat_constant = 8 # 그룹 간 차이(대조 집단 대비 처치 집단)
treat_effect = 13 # 인과 효과
c = np.array([10,15,20,21,22,30,32,38,45,42]) + np.random.normal(size = 10)
t = np.concatenate([c[:5] + treat_constant, c[5:] + treat_constant + treat_effect]) + np.random.normal(size = 10)
t_counterfactual = np.concatenate([t[:5], t[5:] - treat_effect]) # (parallel assumption 만족 시)처치가 없었을 때의 처치 집단의 결과
treated_data = pd.DataFrame({'outcome' : t, 'T_d' : [1] * len(c), 'P_t' : [0,0,0,0,0,1,1,1,1,1]})
control_data = pd.DataFrame({'outcome' : c, 'T_d' : [0] * len(c), 'P_t' : [0,0,0,0,0,1,1,1,1,1]})
data = pd.concat([treated_data, control_data], axis= 0)
data데이터 생김새는 이렇습니다.
- outcome : 결과 변수
- T_d : 처치 여부 (처치를 받은 그룹이면 1, 받지 않은 그룹이면 0)
- P_t : 처치 시점 전/후 (처치 시점 이후는 1, 이전은 0)
| outcome | T_d | P_t |
| 18.076601 | 1 | 0 |
| 24.072336 | 1 | 0 |
| 27.165262 | 1 | 0 |
| 26.883542 | 1 | 0 |
| 30.273883 | 1 | 0 |
| 51.207363 | 1 | 1 |
| 52.592823 | 1 | 1 |
| 57.236814 | 1 | 1 |
| 65.162343 | 1 | 1 |
| 64.267490 | 1 | 1 |
| 9.531791 | 0 | 0 |
| 14.177175 | 0 | 0 |
| 19.934620 | 0 | 0 |
| 20.286638 | 0 | 0 |
| 22.906351 | 0 | 0 |
| 30.766237 | 0 | 1 |
| 32.826054 | 0 | 1 |
| 36.676317 | 0 | 1 |
| 43.247555 | 0 | 1 |
| 43.002449 | 0 | 1 |
각 그룹별로 시점에 따른 트렌드 변화를 살펴보면 아래와 같습니다

- time stamp(x축) : 총 10개의 시점이며 5시점에 처치가 적용됨
- treated : 처치 그룹의 결과
- treated(counterfactual) : 처치 그룹이 처치를 받지 않았을 때의 결과(반사실)
- control : 통제 그룹의 결과
※ 실제로 관측 가능한 데이터는 treated, control 입니다, treated(counterfactual)은 이해를 돕기 위해 "treated 그룹이 처치를 받지 않았을 때(반사실)"을 표현한 것입니다.
그래프에서 보이는 것처럼 처치 이전 시점(0 ~ 5 시점)에 treated, control 결과 변수의 트렌드가 평행한 것을 알 수 있습니다.
parallel assumption을 만족하므로 이중차분법을 활용하여 처치에 의한 인과 효과를 측정할 수 있습니다.
이중 차분 값(인과 효과) 측정
평균 계산
이중 차분을 위해 횡단면(처치 시점 전/후), 종단면(처치 그룹 여부)을 기준으로 결과 변수에 대해 평균값을 계산하면 아래와 같습니다.
| 처치 전 | 처치 후 | |
| 통제 그룹 | 17.367315 (E00) | 37.303723 (E01) |
| 처치 그룹 | 25.294325 (E10) | 58.093366 (E11) |
이를 기준으로 이중 차분 값을 계산하면 (E11−E10)−(E01−E00)=(58.093366−25.294325)−(37.303723−17.367315)=12.86263 로 예제 데이터에서 세팅한 인과 효과(13)과 거의 유사한 값이 도출됩니다.
회귀모델을 이용한 계산
회귀모델을 통해 계산하면 아래와 같습니다
sm.ols('outcome ~ T_d + P_t + T_d * P_t', data).fit().summary().tables[1]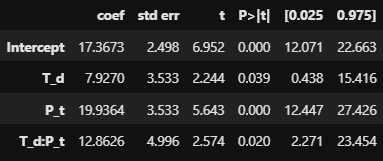
- T_d의 회귀 계수 : 그룹 간 차이(통제 그룹 대비 처치 그룹)
- 세팅한 값인 8과 매우 근접하게 나옵니다
- P_t의 회귀 계수 : 시점 간 차이(처치 전 시점 대비 이후 시점)
- T_d:P_t의 회귀 계수 : 이중 차분 값(인과 효과)
- 세팅한 값인 13과 매우 근접한 값을 가집니다.
- 또한, p-value가 0.020으로 유의한 수준으로 나와 인과 효과가 존재한다고 판단할 수 있습니다.
- 추가로, 위에서 평균 계산을 통해 구한 이중 차분 값과 같습니다
마치며
인과 추론에서 이중차분법에 대한 개념과 측정 방법에 대해 알아보았습니다.
피드백은 언제나 환영합니다
'인과추론(Causal Inference)' 카테고리의 다른 글
| MAB(Multi Armed Bandit) (2) | 2022.03.22 |
|---|---|
| 불연속회귀설계(RDD) 예제 (0) | 2021.10.24 |
| 불연속회귀설계(RDD) (0) | 2021.10.04 |
| 이중차분법(DID) (0) | 2021.10.02 |
| 도구 변수(IV) 예제 (0) | 2021.08.26 |




